Tứ giác nội tiếp – Toán bồi dưỡng lớp 9 – Hình học

Tứ giác nội tiếp Hình học 9

 

Kiến thức cần nhớ:

1. Định nghĩa : Một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn (gọi tắt là tứ giác nội tiếp).

2. Định lí: Trong một tứ giác nội tiếp, tổng số đo hai góc đối bằng .

Đảo lại, nếu một tứ giác có tổng số đo hai góc đối bằng thì tứ giác đó nội tiếp được một đường tròn.

3. Dấu hiệu nhận biết tứ giác nội tiếp

a) Tứ giác có tổng hai góc đối bằng .

b) Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.

c) Bốn đỉnh của tứ giác cách đều một điểm mà ta có thể xác định được.

d) Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc chung a.

4. Chú ý

Để chứng minh nhiều điểm (từ năm điểm trở lên) cùng nằm trên một đường tròn, ta chọn ba điểm nào đó làm gốc rồi chứng minh ba điểm này và một điểm thứ tư là các đỉnh của một tứ giác nội tiếp. Tiếp theo đó ta chứng minh ba điểm gốc này và một điểm thứ năm cũng là các đỉnh của một tứ giác nội tiếp và cứ tiếp tục như vậy đến điểm cuối cùng. Vì qua ba điểm gốc nói trên chỉ có duy nhất một đường tròn nên suy ra tất cả’các điểm đó nằm trên một đường tròn.

Ví dụ 28

Cho tam giác ABC có đường phân giác BN. Từ A kẻ một tia vuông góc với tia BN, cắt BC tại H. Gọi O là tâm đường tròn nội tiếp tam giác ABC. Chứng minh rằng bốn điểm A, O, H, C nằm trên một đường tròn.

Giải vắn tắt.

Ta phân biệt hai trường hợp :

             – H và O nằm cùng phía đối với AC (h.a).

             – H và O nằm khác phía đối với AC (h.b).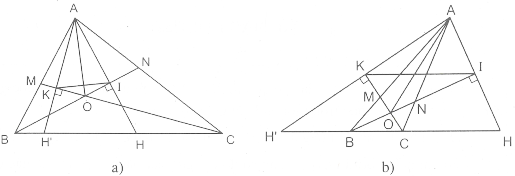

 

Cách 1. AH cắt BN ở I. Kẻ AH’ vuông góc với đường phân giác CM và cắt

CM ở K. Dễ thấy IK là đường trung bình của tam giác AHH’ Từ đó, ta có  bằng (hoặc bù) OCH. Tứ giác AKOI nội tiếp ( =  = ) nên  = . Từ đó suy ra điều phải chứng minh.

Cách 2. Nối OA và OH. Dễ thấy BN là đường trung trực của tam giác ABH.

Suy ra  = , nhưng  = . Do đó  = , ta suy ra điều phải chứng minh.

Cách 3. Tam giác ABI vuông nên  +  = hay  +  +  = .

Suy ra +  +  = hay  =  nên  bằng (hoặc bù) . Từ đó ta có điều phải chứng minh.

Cách 4.  = +  (h.a) hoặc  = –  (h.b).

= +  (vì O là tâm đường tròn nội tiếp). Do đó  bằng (hoặc bù) . Từ đó suy ra điều phải chứng minh.

Cách 5.  =  (góc ngoài ở đỉnh O của tam giác AOB) nên  =  + . Do đó  +  = (h.a) hoặc  =  =  +  (h.b). Từ đó suy ra điều phải chứng minh.

Ví dụ 29

Hai đường, thẳng xy và x’y’ cắt nhau tại M. Trên tia Mx lấy điểm A, trên tia Mx’ lấy điểm C, trên tia My lấy các điểm B và F (B nằm giữa M và F), trên tia My’ lấy các điểm D và E (D nằm giữa M và E). Biết rằng  MA.MB = MC.MD và MD.ME = MB.MF.

Chứng minh rằng :

a) Bốn điểm A, B, C, D cùng thuộc một đường tròn ;

b) Bốn điểm B, D, E, F cùng thuộc một đường tròn ;

c) AC//EF.

Giải.  

 

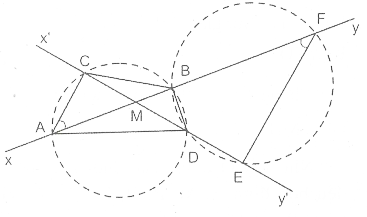
a) Từ giả thiết MA.MB = MC.MD, ta suy ra MA/MD = MC/MB. Lại có  =  (góc đối đỉnh) nên ΔMAC đồng dạng với ΔMDB (c.g.c), do đó = .

Suy ra tứ giác ABCD nội tiếp được một đường tròn.

b) Từ giả thiết  MD.ME = MB.MF, ta suy ra MD/MF = MB/ME, lại có góc M chung nên ΔMDB đồng dạng với ΔMFE (c.g.c), do đó  =                (2).

Suy ra tứ giác BFED nội tiếp được một đường tròn.

c) Từ (1) trong câu a) và (2) trong câu b) suy ra  =  nên AC // EF.

Ví dụ 30

Hai đường tròn () và () cắt nhau ở M và P. Kẻ dây MA của đường tròn () tiếp xúc với đường tròn () ở M. Kẻ dây MB của đường tròn () tiếp xúc với đường tròn () ở M. Trên tia đối của tia PM lấy một điểm H sao cho PH = PM. Chứng minh rằng tứ giác MAHB nội tiếp.

 

Giải.  

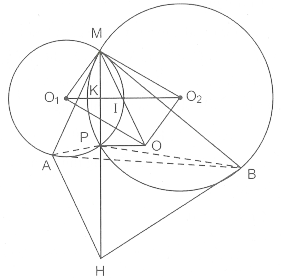
Cách 1.

Từ  và  kẻ các đường vuông góc với MA và MB cắt nhau ở O.

Tứ giác MO là hình bình hành (các cạnh đối song

song từng đôi một) nên I (giao điểm của  và MO) là

trung điểm của MO. Gọi K là giao điểm của  và MP thì K là trung điểm của MP.

Suy ra KI là đường trung bình của tam giác MPO nên KI // PO.

Nhưng KI ⊥ MP (đường nối tâm vuông góc với dây chung MP) do đó OP ⊥ MH.

Như vậy O thuộc các đường trung trực của MH, MA và MB nên O cách đều bốn đỉnh A, M, B, H. Do đó tứ giác MAHB nội tiếp được trong đường tròn (O ; OM).

Cách 2.

Nối PA và PB. Ta có =  (cùng có số đo bằng nửa số đo cung MP) của (),  =  (cùng có số đo bằng nửa số đo cung MP của ()), do đó ΔMAP đồng dạng với ΔBMP (g.g) suy ra AP/AM = MP/MB = PH/MB.                 (1)              

  Ta lại có =  +  =  +  = .                  (2)

Từ (1) và (2) suy ra ΔAPH đồng dạng với ΔAMB (c.g.c). Do đó =  =  . Từ đó suy ra tứ giác MAHB nội tiếp.

 

BÀI TẬP

113. Chứng minh rằng các tứ giác trong các hình vẽ dưới đây nội tiếp được một đường tròn.

 

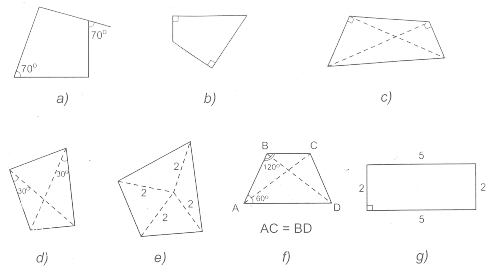
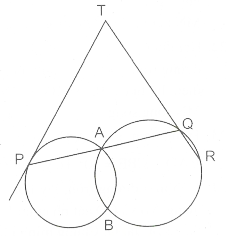
114. Trong hình, PT là một tiếp tuyến của một đường tròn. Chứng minh rằng đường tròn đi qua P, T, R cũng đi qua B.

115. Cho hình thang ABCD nội tiếp đường tròn (O). Các đường chéo AG và BD cắt nhau ở E, các cạnh AD và BC kéo dài cắt nhau ở F.

Chứng minh rằng :

a) Bốn điểm A, D, O, E cùng ở trên một đường tròn;

b) Tứ giác AOCF nội tiếp.

116. Trong góc nhọn AOB lấy một điểm Kẻ CD ⊥ OA, CE ⊥ OB. Từ D và E kẻ DN ⊥ OB, EM ⊥ OA. Chứng minh rằng OC ⊥ MN.

117. Trên cạnh huyền AB của tam giác vuông ABC, dựng hình vuông ABMN có tâm là I. Chứng minh rằng CI là tia phân giác của góc tạo bởi hai đường thẳng AC và BC.

118. Hai cạnh AB và DC của tứ giác ABCD kéo dài cắt nhau tại E, AD và BC kéo dài cắt nhau tại F. Chứng minh rằng các đường tròn ngoại tiếp các tam giác AED, EBC, ABF và CDF cùng đi qua một điểm.

119. Cho tứ giác ABCD nội tiếp đường tròn (O), các đường thẳng BA và CD cắt nhau tại M, BC yà AD cắt nhau tại N. Vẽ đường tròn đi qua ba điểm B, M, N. Đường tròn này cắt đường tròn (O) tại điểm thứ hai B’ (khác B). Chứng minh rằng đường thẳng B’D chia đoạn MN thành hai phần bằng nhau.

120. Cho tam giác đều ABC. Một nửa đường tròn có tâm O nằm trên cạnh BC, tiếp xúc với AC và AB tại K và I. Kẻ một tiếp tuyến với nửa đường tròn cắt các cạnh AB và AC theo thứ tự tại M và N. Đoạn thẳng KI cắt ON và OM theo thứ tự tại P và Q. Chứng minh rằng :

a) MP, NQ là các đường cao của tam giác OMN ;

b) MN = 2PQ.

121. Cho tam giác ABC. Đường phân giác trong của góc B và đường phân giác ngoài của góc C cắt nhau tại M. Đường phân giác ngoài của góc B cắt’đường phân giác trong của góc C tại N. Chứng minh rằng trung điểm P của đoạn MN nằm trên đường tròn ngoại tiếp tam giác ABC.

122. Hai đường tròn () và () cắt nhau ở A và B. Một cát tuyến qua A cắt các đường tròn (), () lần lượt ở M và N. Các tiếp tuyến tại A của () và () theo thứ tự cắt BN và BM ở P và Q. Chứng minh rằng các đường thẳng PQ và MN song song.

123. Trong tam giác ABC, kẻ các đường trung tuyến AD và BE. Biết rằng =  = . Hãy chứng minh rằng AC = BC và = .

124. Trên một đường tròn, lấy bốn điểm A, B, C, D sao cho AB = BD, các đường thẳng AB và CD cắt nhau tại E. Kẻ tiếp tuyến với đường tròn tại A cắt đường thẳng BC tại Q. Chứng minh rằng QE song song với AD.

125. Cho đường tròn (O) và một tiếp tuyến tại A. Trên tiếp tuyến lấy một điểm C (khác A). Gọi B là trung điểm của AC. Kẻ cát tuyến BEF (E và F thuộc (O)). Các tia CE và CF cắt (O) tại M và N. Chứng minh rằng MN song song với AC.

126*. Cho tam giác ABC (CA > CB). Một đường tròn (O) đi qua A và B cắt AC và BC lần lượt ở D và E. M là giao điểm thứ hai của các đường tròn ngoại tiếp các tam giác ABC và DEC. Chứng minh rằng góc OMC vuông.

127. Cho đường tròn (O’) tiếp xúc với các cạnh AB và AC của tam giác ABC và tiếp xúc với đường tròn (O) ngoại tiếp tam giác đó. Chứng minh rằng đoạn thẳng nối các tiếp điểm của đường tròn (O’) trên với các cạnh AB và AC chứa tâm của đường tròn nội tiếp tam giác ABC.

128. Lấy một điểm S nằm trong đường tròn nội tiếp tam giác ABC. Hình chiếu của s trên các cạnh AB, BC và AC lần lượt là ,  và , còn các giao điểm của các tia AS, BS và CS với đường tròn ngoại tiếp lần lượt là ,  và . Chứng minh rằng các tam giác , và  đồng dạng.

129. Trong đường tròn (O ; R), kẻ hai đường kính vuông góc AE và BF. Trên cung EF, lấy một điểm c. Các dây CA và CB cắt các đường kính BF và AE ở P và Q. Chứng minh rằng = .

130. Trong tam giác nhọn ABC, góc B bằng , H là trực tâm, I và K tương ứng là tạm đường tròn nội tiếp các tam giác ABH và CBH. Chứng minh rằng góc nhọn tạo bởi các đường thẳng AK và CI bằng .

131. Cho điểm O thuộc đoạn thẳng AB. Vẽ về một phía của AB các tia Ax, By vuông góc với AB. Các điểm E và F theo thứ tự di chuyển trên các tia Ax và By sao cho  = . Tìm quỹ tích các hình chiếu M của O trên EF.

132. Cho góc vuông xOy và tam giác ABC vuông tại A có  = và BC = a. Tam giác vuông ABC di chuyển trong góc vuông xOy sao cho đỉnh B nằm trên tia Ox, đỉnh c nằm trên tia Oy và đỉnh A khác phía với O đối với BC. Tìm quỹ tích các đỉnh A của tam giác ABC.

133*. Cho tam giác nhọn ABC. Tìm quỹ tích các điểm M sao cho  – ,  – .

134. Trên hai cạnh Ax và Ay của góc nhọn xAy lần lượt lấy hai điểm B và C. Hãy dựng đường tròn đi qua B và C, cắt Ax tại P, cắt Ay tại Q sao cho PQ = m (m là một độ dài cho trước).

135. Cho tam giác nhọn ABC. Hãy dựng điểm E thuộc cạnh BC sao cho đoạn thẳng nối chân các đường vuông góc kẻ từ E đến AB và AC song song với BC.

Xem hướng dẫn giải bài tập tại đây.