Khoảng cách – Bài tập Hình học lớp 11

Khoảng cách

A. CÁC KIẾN THỨC CẦN NHỚ

I. ĐỊNH NGHĨA

1. Cho một điểm O và đường thẳng a. Trong mặt phẳng (O, a) gọi H là hình chiếu của o trên a. Khi đó khoảng cách giữa hai điểm O và H được gọi là khoảng cách từ điểm O đến đường thẳng a, kí hiệu là d(O, a).

2. Khoảng cách từ một điểm o đến mặt phẳng (α) là khoảng cách giữa hai điểm O và H, với H là hình chiếu vuông góc của O lên (α), kí hiệu là d(O, (α)).

3. Khoảng cách giữa đường thẳng a và mặt phẳng (α) song song với a là khoảng cách từ một điểm bất kì thuộc a tới mặt phẳng (α), kí hiệu là d(a, (α)).

4. Khoảng cách giữa hai mặt phẳng song song (α) vằ (β), kí hiệu d((α), (β)), là khoảng cách từ một điểm bất kì của mặt phẳng này đến mặt phẳng kia.

d((α), (β)) = d(M, (β)) với M ∈ (α)

d((α), (β)) = d(N, (α)) với N ∈ (β).

5. Khoảng cách giữa hai đường thẳng chéo nhau là độ dài của đoạn vuông góc chung của hai đường thẳng đó.

II. LƯU Ý

1. Tính khoảng cách có thể áp dụng trực tiếp định nghĩa hoặc tính gián tiếp, chẳng hạn có thể tính được đường cao của một tam giác (khoảng cách từ đỉnh tới đáy) nếu biết diện tích và số đo độ dài cạnh đáy của tam giác đó.

2. Trước khi tính toán, cần xác định rõ yếu tố cần tính khoảng cách.

B. DẠNG TOÁN CƠ BẢN

Vấn đề 1

Tìm khoảng cách từ điểm M đến đường thẳng m cho trước

1. Phương pháp giải

– Trong mặt phẳng xác định bởi điểm M và đường thẳng m ta vẽ MH m tạiH. Ta có d(M, m) = MH. Ta có thể sử dụng các kết quả của hình học phẳng để tính độ dài đoạn MH.

– Trong không gian dựng mặt phẳng ( a) đi qua M và (a) vuông góc với m cắt
m tại H, ta có d(M, m) = MH. Sau đó tính độ dài đoạn MH.

2. Ví dụ

Ví dụ 1. Hình chóp S.ABCD có đáy là hình vuông ABCD tâm O cạnh a, cạnh SA vuông góc với mặt phẳng (ABCD) và SA = a. Gọi I là trung điểm của cạnh SC và M là trung điểm của đoạn AB.

a) Chứng minh đường thẳng 10 vuông góc với mặt phẳng (.ABCD).

b) Tính khoảng cách từ điểm I đến đường thẳng CM.

Giải

a) Ta có SA (ABCD) mà IO // SA do đó IO  (ABCD) (h.3.33).

b) Trong mặt phẳng (ICM) ta dựng IH CM (H ∈ CM). Trong mặt phẳng (ABCD) dựng OH CM, ta có IH CM và IH chính là khoảng cách từ I đến đường thẳng CM.

Gọi N là giao điểm của MO với cạnh CD. Hai tam giác vuông MHO và

Ví dụ 2. Cho tam giác ABC với AB = 7 cm, BC = 5 cm, CA = 8 cm. Trên đường thẳng vuông góc với mặt phẳng (ABC) tại A lấy điểm O sao cho AO = 4 cm.

Tính khoảng cách từ điểm o đến đường thẳng BC.

Giải

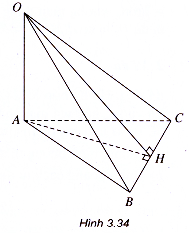
Ta dựng AH BC tại H (h.3.34).

Theo công thức Hê-rông diện tích S của tam giác ABC là

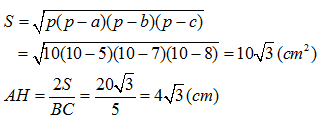
Vì AH  BC nên OH  BC theo định lí ba đường vuông góc.

Ta suy ra = 16 + 48 = 64

Vậy OH = 8cm.

Vấn đề 2 

Tìm khoảng cách từ điểm M đến mặt phẳng (α) 

1. Phương pháp giải

Dựng MH (α) với H ∈ (α) và tính MH.

2. Ví dụ

Ví dụ 1. Cho góc vuông và một điểm M nằm ngoài mặt phẳng chứa góc vuông. Khoảng cách từ M đến đỉnh O của góc vuông bằng 23 cm và khoảng cách từ M tới hai cạnh Ox và Oỵ đều bằng 17 cm. Tính khoảng cách từ M đến mặt phẳng chứa góc vuông.

Giải

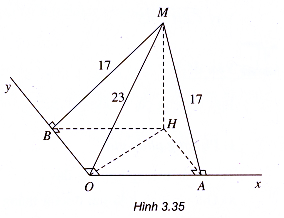
Gọi A và B lần lượt là hình chiếu vuông góc của M trên Ox và Oy (h.3.35).

Ta có MO = 23 cm, MA = MB =17 cm. Gọi H là hình chiếu vuông góc của M trên mặt phẳng (OAB).

Cần tính khoảng cách MH từ M đến mặt phẳng (OAB).

Theo định lí ba đường vuông góc ta có HA OA và HB OB. Do đó tứ giác OAHB là hình chữ nhật. Mặt khác vì MA = MB =  17cm nên HA = HB. Vậy tứ diện OAHB là hình vuông. Đặt OA = x ta có OH = x. Do đó

⇒  ⇒

Vậy nên MH = 7 cm.

Ví dụ 2. Tam giác ABC vuông tại A, có cạnh AB = a nằm trong mặt phẳng (α), cạnh AC = a và tạo với (α) một góc 60°.

a) Tính khoảng cách CH từ c tới (α).

b) Chứng minh rằng cạnh BC tạo với (α) một góc φ = 45°.

Giải

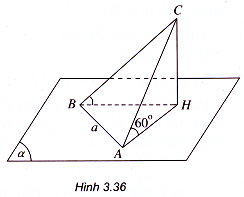
Gọi H là hình chiếu vuông góc của C trên (α). Theo giả thiết ta có = 60°, do đó

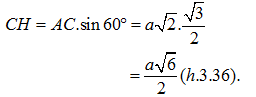
b) Ta có là góc của cạnh BC tạo với mặt phẳng (α).

Vì BA CA nên :

⇒ BC =

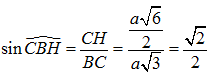
Vậy = 45°.

Vấn đề 3

Tính khoảng cách giữa hai đường thẳng chéo nhau

1. Phương pháp giải

Ta có các trường hợp sau đây :

a) Giả sử a và b là hai đường thẳng chéo nhau và a b

• Ta dựng mặt phẳng (α) chứa a và vuông góc với b tại B.

• Trong (α) dựng BA a tại A, ta được độ dài đoạn AB là khoảng cách giữa hai đường thẳng chéo nhau a và b (h.3.37).

b) Giả sử a và b là hai đường thẳng chéo nhau nhưng không vuông góc với nhau.

Cách 1 :

• Ta dựng mặt phẳng (α) chứa a và song song với b (h.3.38).
• Lấy một điểm M tuỳ ý trên b dựng MM’ (à) tại M\
• Từ M’ dựng b’ // b cắt a tại
• Từ A dựng ABIIMM’ cắt b tại B, độ dài đoạn AB là khoảng cách giữa hai đường thẳng chéo nhau a và

Cách 2 :

• Ta dựng mặt phẳng (α) a tại Oy, (α) cắt b tại I (h.3.39)

• Dựng hình chiếu vuông góc của b là b’ trên (α).
• Trong mặt phẳng (α), vẽ OH b’,H ∈ b’
• Từ H dựng đường thẳng song song với a cắt b tại B
• Từ B dựng đường thẳng song song với OH cắt a tại A

Độ dài đoạn AB là khoảng cách giữa hai đường thẳng chéo nhau a và b.

2. Ví dụ

Ví dụ 1. Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, có cạnh SA = h và vuông góc với mặt phẳng (ẠBCD). góc chung của:

a) SB và CD ;

b)SC và BD ;

c) SC và AB.

Giải

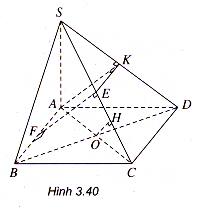
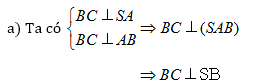
Mặt khác BC CD. Vậy BC là đoạn vuông góc chung của SB và CD.

Khoảng cách giữa SB và CD là đoạn BC = a (h.3.40).

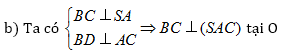
Trong mặt phẳng (SAC) từ o hạ OH SC tại H ta có OH SC và OH BD vì BD (SAC). Vậy OH là đoạn vuông góc chung của BD và SC.

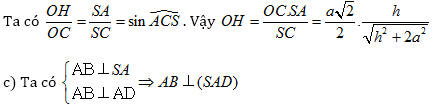
Trong mặt phẳng (SAD) ta có SD là hình chiếu vuông góc của SC, ta vẽ AK SD tại K. Trong mặt phẳng (SCD) vẽ KE // CD với E ∈ SC.

Trong mặt phẳng (KE, AB) vẽ EF // AK vófi F ∈ AB. Ta có AB và CD cùng vuông góc với mặt phẳng (SAD) nên AB AK và CD AK.

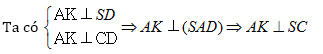
Vậy AK AB và AK SC. Vì EF // AK nên EF AB và EF  SC. Do đó EF là đoạn vuông góc chung của SC và AB.

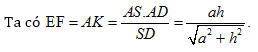
Ví dụ 2. Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = OB = oc = a. Gọi I là trung điểm của BC. Hãy dựng và tính độ dài đoạn vuông góc chung của các cặp đường thẳng :

a) OA và BC

b) AI và OC

Giải

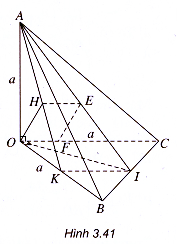
Từ I vẽ IK // OC thì IK vuông góc với mặt phẳng (OAB) tại trung điểm K của đoạn OB. Ta có AK là hình chiếu vuông góc với AI trên mặt phẳng (OAB)

Trong mặt phẳng (OAB) vẽ OH   AK. Dựng HE // OC với E ∈ AI và dựng EF // OH với F ∈ OC. Khi đó EF là đoạn vuông góc chung của AI và OC.

Ta có EF = OH.

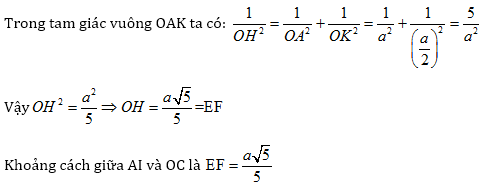
Ví dụ 3. Hình chóp S.ABCD có đáy là hình vuông ABCD có tâm O có cạnh AB = a. Đường cao SO của hình chóp vuông góc với mặt đáy (ABCD) và có SO = a. Tìm khoảng cách giữa hai đường thẳng SC và AB chéo nhau.

Giải

Vì AB // CD nên AB // (SCD). Do đó khoảng cách giữa hai đường thẳng SC và AB chéo nhau bằng khoảng cách giữa AB và mặt phẳng (SCD) chứa SC và song song với AB (h.3.42).

Gọi I, K lần lượt là trung điểm của AB, CD thì ta có o là trung điểm của IK và IK CD.

Do đó :

d(AB, (SCD)) = d(I, (SCD)) = 2d(O, (SCD)).

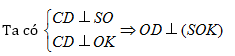
⇒ (SCD) (SOK) với SK = (SCD) ∩ (SOK).

Trong tam giác vuông SOK ta có OH SK nên OH (SCD), do đó

OH = d(O,(SCD)).

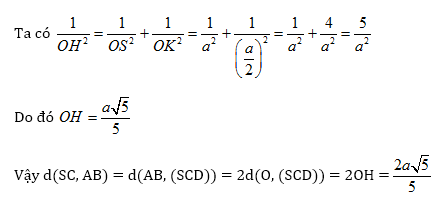
C. CÂU HỎI VÀ BÀI TẬP

3.33. Cho hình lập phương A’B’C’D’ cạnh a. Chứng minh rằng khoảng cách từ các điểm A’, B, D; C, B’, D’ tới đường chéo AC’ bằng nhau. Tính khoảng cách đó.

⇒ Xem đáp án tại đây.

3.34. Hình chóp ABCD có đáy là hình vuông ABCD cạnh á. Các cạnh bên SA = SB = SC = SD = a . Gọi I  và K lần lượt là trung điểm của AD và BC.

a) Chứng minh mặt phẳng (SIK) vuông góc với mặt phẳng (SBC).

b) Tính khoảng cách giữa hai đường thẳng AD và SB.

⇒ Xem đáp án tại đây.

3.35. Cho hình lập phương A’B’C’D’.

a) Chứng minh đường thẳng BC’ vuông góc với mặt phẳng (A’B’CD).

b) Xác định và tính độ dài đoạn vuông góc chung của AB’ và BC’.

⇒ Xem đáp án tại đây.

3.36. Cho hình chóp ABCD có đáy là nửa lục giác đều ABCD nội tiếp trong đường tròn đường kính AD = 2a và có cạnh SA vuông góc với mặt phẳng đáy (ABCD) vớì SA =a.

a) Tính các khoảng cách từ A và B đến mặt phẳng (SCD).

b) Tính khoảng cách từ đường thẳng AD đến mặt phẳng (SBC).

⇒ Xem đáp án tại đây.

3.37. Tính khoảng cách giữa hai cạnh đối trong một tứ diện đều cạnh a.

⇒ Xem đáp án tại đây.

3.38. Tính khoảng cách giữa hai cạnh AB và CD của hình tứ diện ABCD biết rằng AC = BC = AD = BD = a và AB = p, CD = q.

⇒ Xem đáp án tại đây.

3.39. Hình chóp tam giác đều ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Gọi G là trọng tâm của tam giác đáy ABC.

a) Tính khoảng cách từ S tới mặt phẳng đáy {ABC).

b) Tính khoảng cách giữa hai đường thẳng AB và SG

⇒ Xem đáp án tại đây.

3.40. Cho hình lăng trụ tam giác A’B’C’ có tất cả các cạnh bên và cạnh đáy đều bằng a. Các cạnh bên của lăng trụ tạo vói mặt phẳng đáy góc 60° và hình chiếu vuông góc của đỉnh A lên mặt phẳng (A’B’C’) trùng với trung điểm của cạnh B’C’

a) Tính khoảng cách giữa hai mặt phẳng đáy của lăng trụ.

b) Chứng minh rằng mặt bên BCC’B’ là một hình vuông.

⇒ Xem đáp án tại đây.