Đa giác ngoại tiếp, đa giác nội tiếp đường tròn – Toán bồi dưỡng lớp 9 – Hình học

Đa giác nội tiếp đường tròn  

 

Kiến thức cần nhớ:

1. Đường tròn đi qua tất cả các đỉnh của một đa giác gọi là đường tròn ngoại tiếp đa giác và đa giác gọi là nội tiếp đường tròn.

Đường tròn tiếp xúc với tất cả các cạnh của một đa giác gọi là đường tròn nội tiếp đa giác và đa giác gọi là ngoại tiếp đường tròn.

Định lí. Bất kì đa giác đều nào cũng có một đường tròn ngoại tiếp và một đường tròn nội tiếp.

Tâm chung của hai đường trồn này gọi là tâm của đa giác đều.

2. Bổ sung : Tứ giác ngoại tiếp.

Nếu cả bốn cạnh của một tứ giác cùng tiếp xúc với một đường tròn thì tứ giác đó gọi là tứ giác ngoại tiếp đường tròn và đường tròn đó gọi là đường tròn nội tiếp tứ giác.

Định lí. Trong một tứ giác ngoại tiếp, các tổng các cạnh đối thì bằng nhau.

Đảo lại, nếu một tứ giác có các tổng các cạnh đối bằng nhau thì tứ giác đó ngoại tiếp được một đường tròn.

ABCD ngoại tiếp <=> AB + CD = AD + BC.

Ví dụ 31

Một tam giác đều, một hình vuông và một hình lục giác đều cùng nội tiếp đường tròn (O ; R).

Tính độ dài mỗi cạnh của các hình trên theo R.

Chứng tỏ rằng bán kính của đường tròn nội tiếp lục giác đều bằng một nửa cạnh của tam giác đều.

Giải

a) – Xét tam giác đều ABC nội tiếp đường tròn (O ; R). (h.a)

Kẻ đường cao AH, ta có HC = Rsin = .

Do đó BC = 2HC = R.

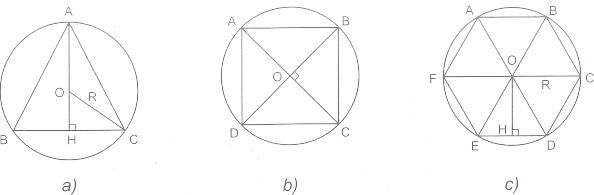
– Xét hình vuông ABCD nội tiếp đường tròn (O ; R). (h.b)

ΔBOC vuông cân nên BC = .

– Xét lục giác đều ABCDEF nội tiếp đường tròn (O ; R). (h.c)

ΔBOC đều nên BC = R.

b) Kẻ OH ⊥ DE (h.c), OH là bán kính của đường tròn nội tiếp lục giác đều.

Ta có OH = OD sin= .

Cạnh của tam giác đều nội tiếp đường tròn (O ; R) bằng , do đó bán kính của đường tròn nội tiếp lục giác đều bằng nửa cạnh của tam giác đều.   

Ví dụ 32

Chứng minh rằng diện tích của một hình thang vuông ngoại tiếp một đường tròn bằng tích của hai cạnh đáy.           

Giải.

Xét hình thang ABCD ngoại tiếp đường tròn (O),  =  = .            

Cách 1.

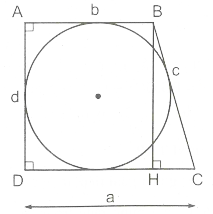
Đặt CD = a, AB = b, BC = c, AD = d. 

Kẻ BH ⊥ CD.        

Trong tam giác vuông BHC ta có

+  =  nên  + = .                            (1)

Do ABCD là tứ giác ngoại tiếp nên a + b = c + d, suy ra c = a + b – d,

do đó  = .                 (2)

 

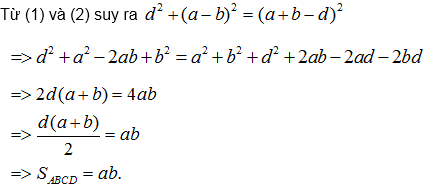
Vậy diện tích hình thang vuông ngoại tiếp một đường tròn bằng tích của hai cạnh đáy.

Cách 2. 

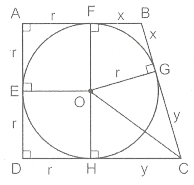
Đặt AF = AE = DE = DH = OF = OE = OH = OG = r.

BF = BG = x, CG = CH = y. Ta có

 

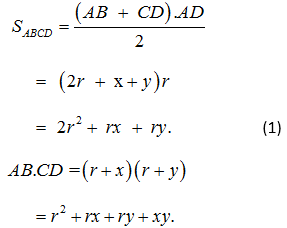
Ta lại có OB, OC là tia phân giác của hai góc kề bù nên OB ⊥ OC.

Do đó  = BG.GC tức là = xy. Suy ra AB.CD = 2 + rx + ry.         (2)

Từ (1) và (2) suy ra = AB.CD.

 

BÀI TẬP

Đa giác ngoại tiếp, đa giác nội tiếp đường tròn

136. Chứng minh rằng trong ngũ giác ABCDE, nếu = ,  =   thì  = .

137. Trong lục giác ABCDEF, các cạnh AB và DE, BC và EF, CD và FA song song. Biết rằng các đường chéo AD, BE, CF bằng nhau. Chứng minh rằng lục giác này có thể nội tiếp được trong một đường tròn.

138. Trong tam giác KIM, hai đường phân giác KN và IP cắt nhau tại Q. Biết rằng PN = 1 cm, đỉnh M nằm trên đường tròn đi qua ba điểm N, P và Q. Tìm số đo các cạnh và các góc của tam giác PNQ.

139. Một đa giác ngoại tiếp một đường tròn bán kính r được chia một cách tuỳ ý thành các tam giác. Chứng minh rằng tổng các bán kính của các đường tròn nội tiếp các tam giác này lớn hơn r.

140. Chứng minh rằng nếu ngũ giác ABCDE có năm cạnh bằng nhau và có  =  =  thì ABCDE là ngũ giác đều.

141. Cho lục giác ABCDEF nội tiếp đường tròn (O). Chứng  minh rằng

+ + =  +  + .

142. Cho lục giác ABCDEF nội tiếp đường tròn (O). Chứng minh rằng nếu AD, BE và CF cắt nhau tại một điểm thì AB.CD.EF = BC.DE.FA.

143. Hãy chia một lục giác đều thành tám phần có diện tích bằng nhau.

144. Cho hai đa giác đều n cạnh  và  theo thứ tự nội tiếp và ngoại tiếp cùng một đường tròn bán kính R. Gọi  là bán kính đường tròn nội tiếp đa giác ,  là bán kính đường tròn ngoại tiếp đa giác . Chứng minh rằng = ..

Tứ giác ngoại tiếp đường tròn

145. Cho một hình thang ngoại tiếp một đường tròn. Chứng minh rằng các đường tròn có đường kính là các cạnh bên tiếp xúc nhau.

146. Một hình thang cân ABCD (AB // CD) ngoại tiếp một đường tròn bán kính R. Tính tích AB.CD theo R.

147. Trong một hình thang, độ dài các đường chéo bằng và , còn độ dài các đáy là 10 và 15. Tìm diện tích hình thang. Hình thang này có thể nội tiếp hoặc ngoại tiếp một đường tròn không ?

148*. Một đường tròn tiếp xúc với hai cạnh và hai đường trung tuýện của một tam giác. Chứng minh rằng tam giác này là tam giác cân.

Xem hướng dẫn giải bài tập tại đây.