Hai đường thẳng vuông góc
A. CÁC KIẾN THỨC CẦN NHỚ
I. TÍCH VÔ HƯỚNG CỦA HAI VECTƠ TRONG KHÔNG GIAN
1. Góc giữa hai vectơ
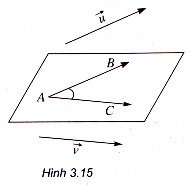
Cho và
là hai vectơ trong không gian. Từ một điểm A bất kì vẽ
=
,
=
. Khi đó ta gọi góc
(0° <
< 180°) là góc giữa hai vectơ
và
, kí hiệu (
,
). Ta có :
(,
) =
(h.3.15).
2. Tích vô hướng
Trong không gian, tích vô hướng của hai vectơ khác vectơ không và
là một số được kí hiệu là
.
xác định bởi:
.
= |
|. |
| .cos(
,
) Nếu
=
hoặc
=
thì ta quy ước
.
=0.
3. Tính chất
Với ba vectơ ,
,
bất kì trong không gian và với mọi số k ta có :
.
=
.
(tính chất giao hoán);
.(
+
) =
.
+
.
(tính chất phân phối đối với phép cộng vectơ);
- (k
).
= k(
.
) =
.k
;
≥ 0;
⇔
=
.
4. Vectơ chỉ phương của đường thẳng
- Vectơ
≠
được gọi là vectơ chỉ phương của đường thẳng d nếu giá của vectơ
song song hoặc trùng với đường thẳng
- Nếu
là vectơ chỉ phương của đường thẳng d thì vectơ kã với k ≠ 0 cũng là vectơ chỉ phương của d.
- Một đường thẳng d trong không gian hoàn toàn được xác định nếu biết một điểm A thuộc d và một vectơ chỉ phương
của d.
5. Một số ứng dụng của tích vô hướng
![]()
- Xác định góc giữa hai vectơ
và
bằng cos (
,
) theo công thức :
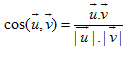
II. GÓC GIỮA HAI ĐƯỜNG THẲNG
Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm bất kì lần lượt song song vói a và b.
III. HAI ĐƯỜNG THẲNG VUÔNG GÓC
- Hai đường thẳng a và b được gọi là vuông góc với nhau nếu góc giữa chúng bằng 90°. Ta kí hiệu a
b hoặc b
a
- Nếu
và
lần lượt là các vectơ chỉ phương của hai đường thẳng a và b thì a
b ⇔
.
= 0.
- Nếu a // b và c vuông góc với một trong hai đường thẳng đó thì c vuông góc với đường thẳng còn lại.
B. DẠNG TOÁN CƠ BẢN
Vấn đề 1
Ứng dụng của tích vô hướng
1. Phương pháp giải
a) Muốn tính độ dài của đoạn thẳng AB hoặc tính khoảng cách giữa hai điểm
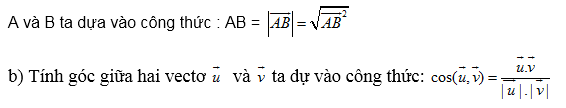
c) Chứng minh hai đường thẳng AB và CD vuông góc với nhau ta cần chứng minh .
= 0 .
2. Ví dụ
Ví dụ 1. Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi O là tâm của hình vuông ABCD và s là một điểm sao cho :
=
+
+
+
+
+
+
+
.
Hãy tính khoảng cách giữa hai điểm O và S theo a.
Giải
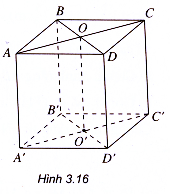
Ta có: +
=
;
+
=
và +
= 2
;
+
= 2
với O’ là tâm của hình vuông A’B’C’D’ (h.3.16).
Do đó: =
+
+
+
= 4 mà |
| = a.
Vậy || = 4a.
Ví dụ 2. Trong không gian cho hai vectơ và
tạo với nhau một góc 120°. Hãy tìm |
+
| và l
–
| biết rằng |
| = 3 cm và |
| = 5 cm.
Giải
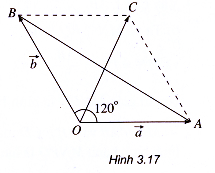
Từ một điểm o trong không gian dựng =
và
=
với
= 120° (h.3.17).
Sau đó ta dựng hình bình hành OACB.
Ta có =
+
và
=
–
=
–
.
- Xét tam giác OAC ta có
= 60° và
– 2.OA.ACcos60° = 9 + 25 – 2.3.5. 1/2 = 19.
Vậy | =|
=19.
Do đó =
(cm).
- Xét tam giác OAB ta có :
– 2.OA.0B cos 120°
= 9 + 25 -2.3.5.(-1/2) = 49.
Vậy | =|
=49
Do đó =7 (cm).
Ví dụ 3. Cho tứ diện ABCD có hai mặt ABC và ABD là hai tam giác đều.
a) Chứng minh rằng AB và CD vuông góc với nhau.
b) Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AC, BC, BD, DA. Chứng minh rằng tứ giác MNPQ là hình chữ nhật.
Giải
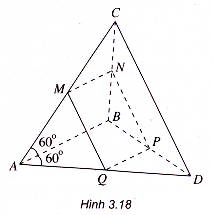
a) Ta có .
= (
–
)
=
.
–
.
.
Đặt AB = a ta có AD = AB = AC = a (h.3.18).
Do đó, .
= I
I.I
Icos60° – I
II
I.cos60°
Vậy CD AB
b) Ta có MN // PQ //AB
![]()
nên tứ giác MNPQ là hình bình hành.
Vì MN // AB và NP // CD mà AB CD nên hình bình hành MNPQ là hình chữ nhật.
Vấn đề 2
Chứng minh hai đường thẳng vuông góc với nhau
1. Phương pháp giải
- Cần khai thác các tính chất về quan hệ vuông góc đã biết trong hình học phẳng.
- Sử dụng trực tiếp định nghĩa góc của hai đường thẳng trong không gian.
- Muốn chứng minh hai đường thẳng AB và CD vuông góc với nhau ta có thể chứng minh
.
= 0.
2. Ví dụ
Ví dụ 1. Cho hai vectơ và
đều khác vectơ
. Chứng minh rằng
và
là hai vectơ chỉ phương của hai đường thẳng vuông góc với nhau khi và chỉ khi
| +
| = |
–
|
Giải
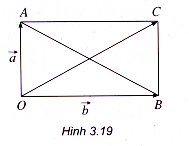
Từ một điểm O trong không gian ta vẽ =
,
=
) rồi vẽ hình bình hành OACB (h.3.19).
Ta có: –
+
=
+
=
–
–
–
.
Từ đó ta suy ra | +
| – |
–
| khi và chỉ khi |
| = |
|. hay OC = BA nghĩa là khi và chỉ khi OACB là hình chữ nhật. Khi đó
và
có giá là hai đường thẳng vuông góc với nhau.
Ví dụ 2. Cho tứ diện đều ABCD cạnh a. Gọi o là tâm đường tròn ngoại tiếp tam giác BCD. Chứng minh đường thẳng AO vuông góc với đường thẳng CD.
Giải
Ta có:
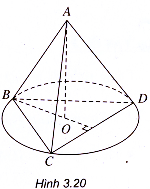
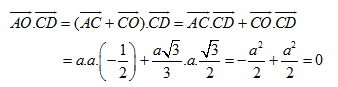
Do đó AO CD (h.3.20)
Ví dụ 3. Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Trên các cạnh DC và BB’ ta lần lượt lấy các điểm M và N sao cho DM = BN = x vói 0 ≤ x ≤ a. Chứng minh rằng hai đường thẳng AC’ và MN vuông góc với nhau.
Giải
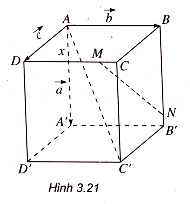
Đặt =
,
=
,
=
(h.3.21).
Ta có || = |
| = |
| = a và
=
+
+
hay =
+
+
Mặt khác =
–
= ( +
) – (
+
)
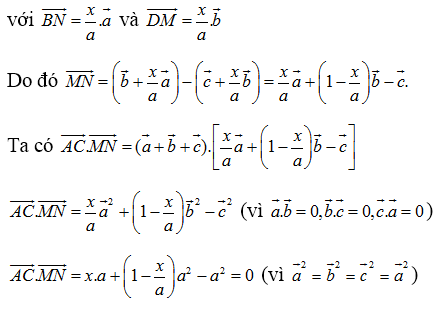
Do đó AC’ MN
Vấn đề 3
Dùng tích vô hướng để tính góc của hai đường thẳng trong không gian
1. Phương pháp giải
- Muốn tính góc (
,
) ta có thể dựa vào công thức
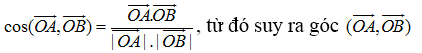
Đặc biệt nếu .
= 0 ta có (
,
) = 90°.
- Nếu
là vectơ chỉ phương của đường thẳng a và
là vectơ chỉ phương của đường thẳng b và (
,
) = a thì góc giữa hai đường thẳng a và b bằng a nếu a ≤ 90° và bằng 180° – a nếu a > 90°.
2. Ví dụ
Ví dụ 1. Cho hình lập phương ABCD.A’B’C’D’.
a) Tính góc giữa hai đường thẳng AC và DA’.
b) Chứng minh BD AC’
Giải
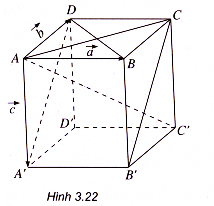
a) Đặt =
,
=
,
=
(h.3.22).
Ta có =
+
=
+
=
–
=
–
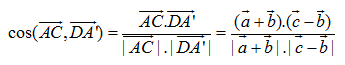
Giả sử hình lập phương có cạnh bằng x ta có :
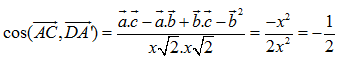
(vì .
= 0,
.
= 0,
.
= 0 và
).
Vậy (,
) = 120°.
Ta suy ra góc giữa hai đường thẳng AC và DA’ bằng 60°.
Cách khác. Từ đỉnh C, nối CB’ ta có CB’ // DA’. Góc giữa AC và DA’ chính là góc giữa AC và CB’. Ta có ACB’ là tam giác đều có độ dài mỗi cạnh bằng nên góc
= 60° hay góc giữa hai đường thẳng AC và DA’ bằng 60°.
b) Ta cần tính góc giữa hai vectơ và
.
Ta có =
–
,
=
+
+
.
Vậy .
= (
–
).(
+
+
) = (
–
).(
+
+
)
= .
+
+
.
–
–
.
–
.
= 0 + + 0 –
+ 0 – 0 = 0.
Vậy BD AC’
Ví dụ 2. Cho tứ diện đều ABCD canh a. Tính góc giữa hai đường thẳng AB và CD.
Giải
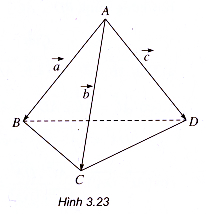
Đặt =
,
=
,
=
.
Ta có =
–
=
–
.
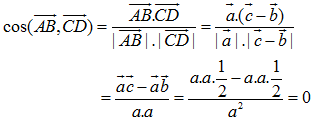
vì || = |
| = |
| = a
Vậy (,
) = 90° (h.3.23).
C. CÂU HỎI VÀ BÀI TẬP
3.8. Cho tứ diện Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng .
+
.
+
.
= 0.
3.9. Cho tứ giác Gọi M, N, P, Q lần lượt là trung điểm của các đoạn AC, BD, BC, AD và có MN = PQ. Chứng minh rằng AB CD.
3.10. Cho hình chóp tam giác ABC có SA = SB = SC = AB = AC = a và BC = Tính góc giữa hai vectơ
và
.
3.11. Cho hình chóp S.ABC có SA = SB = SC = AB = AC = a và BC = . Tính góc giữa hai đường thẳng AB và SC.
3.12. Chứng minh rằng một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
3.13. Cho hình hộp A’B’C’D’ có tất cả các cạnh đều bằng nhau (hình hộp như yậy còn được gọi là hình hộp thoi). Chứng minh rằng AC B’D’.
3.14. Cho hình hộp thoi A’B’C’D’ có tất cả các cạnh bằng a và =
=
= 60°. Chứng minh tứ giác A’B’CD là hình vuông.
3.15. Cho tứ diện ABCD trong đó AB AC, AB
BD. Gọi P và Q lần lượt là trung điểm của AB và Chứng minh rằng AB và PQ vuông góc với nhau.


Comments mới nhất