Cung chứa góc – Toán bồi dưỡng lớp 9 – Hình học

Cung chứa góc  Hình học 9

 

Kiến thức cần nhớ:

     Quỹ tích các điểm nhìn một đoạn thẳng cho trước dưới một góc a không đổi là hai cung chứa góc a dựng trên đoạn thẳng đó.

      Quỹ tích các điểm nhìn đoạn thẳng AB cho trước dưới một góc vuông là đường tròn đường kính AB.

Ví dụ 26

Cho nửa đường tròn (O) đường kính AB, C là điểm chính giữa của cung AB. M là một điểm chuyển động trên cung CB. Gọi H là hình chiếu của c trên AM. Các tia OH và BM cắt nhau tại I. Tìm quỹ tích các điểm I.  

Giải. 

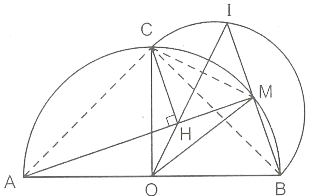
Phần thuận :

Ta có số đo cung AC =  nên  = . Do đó tam giác CHM vuông cân tại H, HC = HM. Ta lại có OC = OM nên OH là đường trung trực của CM.

Điểm I thuộc tia OH nên IC = IM, do đó tam giác CIM cân tại I. Ta có  = ,  =  nên  = . Suy ra tam giác CIM vuông cân,  = .

Điểm I nhìn đoạn BC cố định dưới góc vuông nên I nằm trên đường tròn đường kính BC.

Giới hạn : Khi M trùng B thì I trùng B. Khi M trùng C thì I trùng C. Điểm I chỉ nằm trên nửa đường tròn đường kính BC (phần nằm ngoài đường tròn tâm O).

Phần đảo :

Lấy điểm I bất kì thuộc nửa đường tròn đường kính BC (phần nằm ngoài đường tròn tâm O). IB cắt nửa đường tròn (O) ở M. Kẻ CH ⊥ AM. Ta có  = ,  =  nên  = .

Tứ giác CHMI có ba góc vuông nên là hình chữ nhật, lại có MC là đường phân giác của góc M nên CHMI là hình vuông, suy ra HC = HM, IC = IM. Ta lại có OC = OM nên các điểm H, I, O đều nằm trên đường trung trực của CM, tức là các tia OH và BM cắt  nhau tại I.

Kết luận : Quỹ tích các điểm I là nửa đường tròn đường kính BC, phần nằm ngoài nửa đường tròn (O).

Ví dụ 27

Cho hình bình hành ABCD. Tia phân giác của góc D cắt các đường thẳng AB, BC theo thứ tự ở I, K. Gọi O là tâm đường tròn ngoại tiếp tam giác BIK. Chứng minh rằng :

a) OB vuông góc với IK ;

b) Điểm O nằm trên đường tròn ngoại tiếp tam giác ABC.

Giải.  

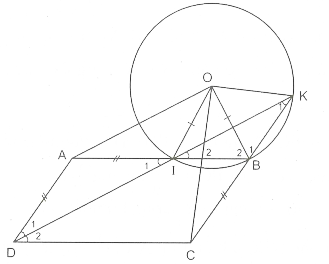
Hình 54

a) Ta có AD // BC nên  =  , AB // CD nên  =  = . Theo giả thiết  =  nên  = . Suy ra BI = BK, do đó OB ⊥ IK.

b) BO là đường trung trực của tam giác cân BIK nên  = . Ta lại có

 =  nên  = . Suy ra các góc kề bù với chúng bằng nhau, tức là = .

Các tam giác OBC và OIA có OB = OI, BC = IA (cùng bằng AD),

= nên ΔOBC = ΔOIA (c.g.c), suy ra =  tức là  = .

Các điểm C và A nằm về một phía của OB, cùng nhìn OB dưới hai góc bằng nhau nên nằm trên cùng một cung chứa góc dựng trên OB, tức là điểm O nằm trên đường tròn ngoại tiếp tam giác ABC.

 

BÀI TẬP

108. Cho đường tròn (O) có đường kính AB cố định. Một điểm C chạy trên đường tròn. Kẻ CD vuông góc với AB. Trên OC đặt một đoạn OM = CD. Tìm quỹ tích các điểm M.

109. Cho nửa đường tròn đường kính AB. M là một điểm chuyển động trên nửa đường tròn đó. Vẽ hình vuông BMDC ở ngoài tam giác AMB. Tìm quỹ tích điểm C.

110. Cho tam giác ABC vuông tại A. Gọi (I) là đường tròn nội tiếp tam giác. M, N là các tiếp điểm trên AC, BC. Gọi H là giao điểm của AI và MN. Chứng minh rằng điểm H thuộc đường tròn đường kính BI.

111. Dựng hình vuông ABCD biết đỉnh A và trung điểm M của cạnh BC.

112. Cho tam giác ABC cố định vuông tại B có AC = b. Các tia phân giác của góc A và góc C cắt nhau ở I. Chứng minh rằng điểm I nằm trên một đường tròn cố định có bán kính là b.

Xem hướng dẫn giải bài tập tại đây.