Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu – Sách bài tập Toán 7 tập II

Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu – Sách bài tập Toán 7 tập II

ĐỀ BÀI:

Bài 11.

Cho hình 1. So sánh độ các độ dài AB, AC, AD, AE.

Bài 12.

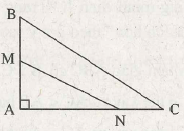
Cho hình 2. Chứng minh rằng MN < BC

 Bài 13.

Cho tam giác ABC cân tại A có AB = AC = 10cm, BC = 12cm. Vẽ cung tròn tâm A có bán kính 9cm. Cung đó có cắt đường thẳng BC hay không có cắt cạnh BC hay không? Vì sao?

Bài 14

Cho tam giác ABC, điểm D nằm giữa A và C (BD không vuông góc với AC). Gọi E và F là chân các đường vuông góc kẻ từ A và C đến đường thẳng BD. So sánh AC với tổng AE + CF.

Bài 15.

Cho tam giác ABC vuông tại A, M là trung điểm của AC. Gọi E và F là chân các đường vuông góc kẻ từ A và C đến đường thẳng BM. Chứng minh rằng  AB < ( BE + BF ) / 2.

Bài 16.

Cho tam giác ABC cân tại A, điểm D nằm giữa B và C. Chứng minh rằng độ dài AD nhỏ hơn cạnh bên của tam giác ABC.

Bài 17.

Cho hình 3 trong đó AB > AC. Chứng minh rằng EB > AC.

Bài 18.

Cho hình 4 . Chứng minh rằng: BD + CE < AB  + AC.

BÀI TẬP BỔ SUNG:

Bài 2.1.

Cho đường thẳng d và điểm A không thuộc d. Trong các khẳng định sau đây, khẳng định nào đúng, khẳng định nào sai?

(A) Có duy nhất một đường vuông góc kẻ từ điểm A đến đường thẳng d

(B)  Có duy nhất một đường kẻ xiên kẻ từ điểm A đến đường thẳng d.

(C)  Có vô số đường vuông góc kẻ từ điểm A đến đường thẳng d.

(D) Có vô số đường kẻ xiên kẻ từ điểm A đến đường thẳng d.

Hãy vẽ hình minh họa cho các khẳng định đúng.

Bài 2.2.

Qua điểm A không thuộc đường thẳng d, kẻ đường vuông góc AH  và các đường xiên AB, AC đến đường thẳng d (H, B, C đều thuộc d). Biết rằng HB < HC. Hãy chọn khẳng định đúng trong các khẳng định sau:

(A) AB > AC               (B) AB = AC

(C) AB > AC               (D) AH > AB

Bài 2.3.

a) Hai tam giác ABC, A’B’C’ vuông tại A và A’ có AB = A’B’, AC > A’C’. Không sử dụng định lý Pitago, chứng minh rằng BC > B’C’.

b) Hai tam giác ABC, A’B’C’ vuông tại A và A’ có AB = A’B’, BC > B’C’.

sử dụng định lý Pytago, chứng minh rằng AC > A’C’

Bài 2.4.

Cho tam giác ABC vuông tại A. Gọi BD là đường phân giác của góc B (D ∈ AC). Chứng minh rằng BD > BC.

Bài 2.5.

Cho điểm A nằm ngoài đường thẳng xy

a) Tìm trên đường thẳng xy hai điểm M, N sao cho hai đường xiên AM và AN bằng nhau.

b) Lấy một điểm D trên đường thẳng xy. Chứng minh rằng:

– Nếu D ở giữa M và N thì AD < AM ;

– Nếu D không thuộc đoạn thẳng MN thì AD > AM.

Bài 2.6.

a) Hãy nêu cách vẽ đường xiên PQ, PR sao cho PQ = PR và  gó${QPR}^{}={60}^{\circ .}$

b) Trong hình dựng được ở câu a), cho PQ = 18cm. Tính độ dài hình chiếu của hai đường xiên PQ, PR trên d.

Xem thêm: Quan hệ giữa góc và cạnh đối diện trong một tam giác  

LỜI GIẢI, CHỈ DẪN HOẶC ĐÁP SỐ:

Bài 11.

(h.31) AB < AC (đường vuông góc ngắn hơn đường xiên).

BC < BD < BE => AC < AD < AE (quan hệ giữa đường xiên và hình chiếu).

Vậy AB<AC<AD<AE.

Bài 12.

(h. 32)

Hình chiếu AN < hình chiếu AC => đường xiên BN < đường xiên BC. (1)

Hình chiếu AM < hình chiếu AB => đường xiên NM < đường xiên NB. (2)

Từ (1) và (2) suy ra :

MN < BN < BC.

Bài 13.

(h.33)

Kẻ AH  ⊥ BC.

tam giác AHB = tam giác AHC ( cạnh huyền – cạnh góc vuông)

nên :

HB = HC = BC/2 = 6 cm.

Xét tam giác  AHC vuông tại H. Theo định lí Py-ta-go :

Do 9cm > 8cm nên cung tròn tâm A bán kính 9cm cắt đường thẳng BC.

Gọi D là giao điểm của cung đó với đường thẳng BC (giả sử D và C nằm cùng phía vói H trên đường thẳng BC).

Đường xiên AD nhỏ hơn đường xiên AC nên hình chiếu HD nhỏ hơn hình chiếu HC. Do đó D nằm giữa H và c. Vậy cung tròn tâm A nói trên cắt cạnh BC.

 

Bài 14.

(h. 34)

Xét tam giác ADE vuông  tại E :

AE < AD                   (1)

Xét tam giác CDF vuông tại F :

CF < CD                    (2)

Từ (1) và (2): AE + CF < AD + CD = AC

 

Bài 15.

(h.35)

Tam giác ABM vuông góc tại A =AB < BM.

Do đó:                   AB < BE + M

và                           AB < BF – MF

tam giác MAE = tam giác MCF (cạnh huyền – góc nhọn)

=> ME = MF. (3)

Từ (1), (2), (3) suy ra

AB + AB < BE + B

Do đó

2AB < BE + BF nên AB < ( BE + BF ) / 2.

Bài 16.

(h.36)

Kẻ AH  ⊥ BC.

– Nếu D trùng H thì AD < AC VÌ AH < AC (đường vuông góc nhỏ hơn đường xiên).

– Nếu D không trùng H, giả sử D nằm giữa H và Ta có HD < HC

=> AD < AC (hình chiếu nhỏ hơn thì đường xiên nhỏ hơn).

Vậy AD nhỏ hơn cạnh bên của A ABC

Bài 17.

(h. 37)

AB > AC  => HB > HC (đường  xiên lớn hơn thì hình  chiếu lớn hơn).

HB > HC => EB > EC (hình chiếu lớn hơn thì đường xiên lớn hơn).

 

Bài 18.

(h. 38)

tam giác ABD vuông tại D =>  BD       <   AB.

Tam giác  ACE vuông tại E => CE < AC.

Suy ra : BD + CE < AB + AC.

BÀI TẬP BỔ SUNG:

Bài 2.1.

Ta biết rằng có duy nhất một đường thẳng đi qua một điểm cho trước, vuông góc vói một đường thẳng cho trước và có vô số đường thẳng đi qua một điểm cho trước cắt một đường cho trước. Bởi vậy, có duy nhất một đường vuông góc kẻ từ điểm A đến đường thẳng d và có vô số đường xiên kẻ từ điểm A đến đường thẳng d.

A. Đúng                  B. Sai                     C. Sai                   D. Đúng

Trong hình bs.4, AH là đường vuông góc (duy nhất)    và AB,    AC,   AD,

AE, AG là những đường xiên kẻ từ A đến   d (có    thể    kẻ được  vô số đường

xiên như thế).

Bài 2.2.

Theo định lí so sánh giữa hình chiếu và đường xiên ta có

HB < HC => AB < AC. Chọn (C).

Bài 2.3.

a) (h.bs.5)

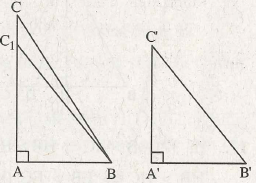
Do AC > A’C’ nên lấy được điểm C1 ’ trên cạnh AC sao cho AC₁ = A’C’.

Ta có tam giác vuông ABC₁ bằng tam giác vuông A’B’C’, suy ra B’C’ = BC1.

Mặt khác hai đường xiên BC và BC1 kẻ từ B đến đường thẳng AC lần lượt có hình chiếu trên AC là AC và AC1 . Vì AC > AC1 nên BC > BC1 , suy ra BC > B’C.

b) Dùng phản chứng :

• Giả sử AC < A’C’. Khi đó theo chứng minh câu a) ta có BC < B’C’. Điều này không đúng với giả thiết BC > B’C’.
• Giả sử AC = A’C’. Khi đó ta có AABC = AA’B’C’ (c.g.c). Suy ra BC = B’C. Điều này cũng không đúng với giả thiết BC > B’C’. Vậy ta phải có AC > A’C’.

(Nếu sử dụng định lí Py-ta-go thì có thể giải bài toán như sau :

Trong tam giác vuông ABC có BC² = AB² + AC².

Trong tam giác vuông A’B’C’ có B’C’² = A’B’² + A’C’².

Theo giả thiết AB = A’B’ nên từ (1), (2) ta có :

Nếu AC > A’C’ thì AC² > A’C², suy ra BC² > B’C’² hay BC > B’C’;

Nếu BC > B’C’ thì BC² > B’C’², suy ra AC² > A’C’² hay AC > A’C’).
Bài 2.4

(h.bs.6)

Do BD là tia phân giác của góc ABC nên tia BD ở giữa hai tia BA và BC, suy ra D ở giữa A và c, hay AD < AC.

Hai đường xiên BC, BD lần lượt có hình chiếu trên AC là AC và AD. Hơn nữa AD < AC, suy ra BD < BC. (Một cách tương tự, ta cũng chứng minh được đoạn thẳng nối B với trang điểm của đoạn thẳng AC nhỏ hơn BC).

Bài 2.5.

a) Phân tích bài toán : Giả sử M và N là hai điểm của đường thẳng xy mà AM = AN. Nếu gọi H là chân đường vuông góc kẻ từ điểm A đến xy thì HM, HN lần lượt là hình chiếu của các đường xiên AM, AN.Từ AM = AN suy ra HM = HN, từ đó xác định được hai điểm M, N.

 Giải (h.bs.7)

Kẻ AH vuông góc với xy (H ∈  xy).

Lấy hai điểm M, N trên xy sao cho HM = HN. (1)

(Dùng compa vẽ một đường tròn tâm bán kính tuỳ ý ; đường tròn này cắt đường thẳng xy tại hai điểm M, N thoả mãn HM = HN).

Hai đường xiên AM, AN lần lượt có bình chiêu là HM và HN, do đó từ (1) suy ra AM = AN.

b) Xét trường hợp D ở giữa M và N.

• Nếu D = H thì AD = AH, suy ra AD < AM (đường vuông góc ngắn hơn đường xiên).
• Nếu D ở giữa M và H thì HD .< HM, do đó AD < AM (đường xiên có hình chiếu ngắn hơn thì ngắn hơn).
• Nếu D ở giữa H và N thì HD < HN, do đó AD < AN.

Theo a) ta có AM = AN nên AD < AM.

Vậy khi D ở giữa M vàN thì ta luôn có AD < AM.

Xét trường hợp D không thuộc đoạn thẳng MN (D  ∈  xy). Khi đó HD > HM (hoặc HD > HN) nên AD > AM.

Bài 2.6.

a) Phân tích bài toán

Giả sử PQ và PR là hai đường xiên kẻ từ p đến d sao cho PQ = PR và góc QPR = 60°. Gọi H là chân đường vuông góc kẻ từ p đến d.

Khi đó tam giác PHQ = tam giác PHR (cạnh huyền, cạnhgóc vuông), suy ra góc HPQ = góc HPR = 30°.

Từ đó ta suy ra cách vẽ hai đường  xiên PQ và PR.

Giải (h.bs.8)

Kẻ PH ⊥ d (H  ∈ d). Dùng thước đo góc để vẽ góc HPx bằng 30°. Tia Px cắt d tại điểm Q. Trên d lấy điểm R sao cho HR = HQ. Hai đường xiên PQ và PR lần lượt có hình chiếu trên d là  HQ và HR. Do HQ = HR nên PQ = PR.

Hơn nữa góc QPR = 2 lần góc HPQ = 60°

b) Hướng dẫn

• Tam giác PQR có PQ = PR và QPR = 60°, tam giác đó là tam giác gì ?

• PQ = 18cm => QR = ? ; HQ = HR = ?