Mặt cầu – Các dạng toán cơ bản – Sách bài tập hình học 12

Jan 16th, 2018 · 1 Comment
Đang tải...

 Các dạng toán cơ bản về mặt cầu – Hình học 12

VẤN ĐỀ 1:

Xác định tâm và bán kính của mặt cầu thoả mãn một số điều kiện cho trước

1. Phương pháp giải

Muốn xác định tâm và bán kính của mặt cầu chúng ta cần dựa vào các mệnh đề sau đây :

a) Tập hợp tất cả những điểm M trong không gian cách điểm O cố định một khoảng bằng r cho trước là mặt cầu tâm o bán kính r ;

b) Tập hợp tất cả những điểm M nhìn đoạn thẳng AB cố định dưới một góc vuông là mặt cầu đường kính AB;

c) Tập hợp tất cả những điểm M sao cho tổng bình phương các khoảng cách từ M tới hai điểm A, B cố định bằng một hằng số  k^{2}   là mặt cầu có tâm là trung điểm O của đoạn AB và bán kính  r=\frac{1}{2}\sqrt{2k^{2}-AB^{2}} .

d) Mặt cầu là mặt tròn xoay được tạo nên bởi một nửa đường tròn quay quanh trục là đường kính AB của nửa đường tròn đó.

2. Ví dụ

Ví dụ 1. Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Hãy xác định tâm và bán kính của mặt cầu trong các trường hợp sau đây :

a) Đi qua 8 đỉnh của hình lập phương ;

b) Tiếp xúc với 12 cạnh của hình lập phương ;

c) Tiếp xúc với 6 mặt bên của hình lập phương.

Giải

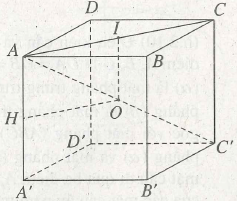
a) (h.2.8) Gọi O là trung điểm của đường chéo AC’. Ta có O cách đều 8 đỉnh của hình lập phương. Vậy mặt cầu đi qua 8 đỉnh của hình lập phương cạnh a có tâm O là trung điểm của đường chéo AC’ và có bán kính  r=\frac{a\sqrt{3}}{2}   .

b) Gọi H là trung điểm của cạnh  AA’.

Ta có OH = \frac{1}{2} AC =  r=\frac{a\sqrt{2}}{2} . Vậy mặt cầu tiếp xúc với 12 cạnh của hình lập phương là mặt cầu có tâm o là trung điểm của đường chéo AC’ và bán kính  r'=OH=\frac{a\sqrt{2}}{2} .

c) Gọi I là tâm của hình vuông Ta có OI = \frac{a}{2} .  Vậy mặt cầu tiếp xúc với 6 mặt bên của hình lập phương là mặt cầu có tâm o là trung điểm của đường chéo AC’ và có bán kính r” bằng khoảng cách từ o tới 6 mặt bên của hình lập phương. Ta có r” = \frac{a}{2}

Ví dụ 2. Chứng tỏ rằng có vô số mặt cầu đi qua hai điểm cố định A, B cho trước. Tìm tập hợp tâm các mặt cầu đó.

Giải

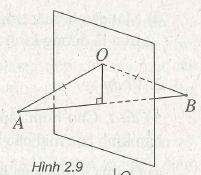
(h.2.9) Điều kiện cần và đủ để o là tâm mặt cầu đi qua hai điểm cố định A và B là OA = OB. Điều này chứng tỏ điểm o thuộc mặt phẳng trung trực của đoạn AB.

Vậy có vô số mặt cầu đi qua hai điểm A, B cho trước và tâm các mặt cầu đó thuộc mặt phẳng trung trực của đoạn AB.

Ví dụ 3. Chứng tỏ rằng có vô số mặt cầu đi qua ba đỉnh A, B, c của một tam giác cố định cho trước. Tìm tập hợp tâm các mặt cầu đó.

Giải

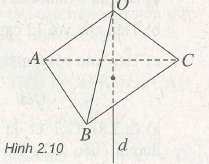
(h.2.10) Điều kiện cần và đủ để cho điểm o là tâm của mặt cầu đi qua ba điểm A, B, C là OA = OB = OC. Điều này chứng tỏ điểm o thuộc mặt phẳng (α) là mặt phẳng trung trực của đoạn AB, đồng thời điểm o cũng thuộc mặt phẳng ( β) là mặt phẳng trung trực của đoạn BC. Vì (α) và (β) cùng vuông góc với mặt phẳng (ABC) và ba điểm A, B, C không thẳng hàng nên mặt phẳng (α) và mặt phẳng (β) cắt nhau theo một giao tuyến d. Vậy có vô số mặt cầu đi qua ba điểm A, B, c cố định không thẳng hàng cho trước và tâm của các mặt cầu ấy nằm trên đường thẳng d vuông góc với mặt phẳng (ABC) tại tâm đường tròn ngoại tiếp tam giác ABC. Người ta thường gọi d là trục của tam giác ABC.

VẤN ĐỀ 2

Xét vị trí tương đối của mặt cầu và mặt phẳng

1. Phương pháp giải

Cần xác định khoảng cách d từ tâm o của mặt cầu đến mặt phẳng (P) và so sánh với bán kính r của mặt cầu cho trước.

– Nếu d> r, mặt phẳng (P) không cắt mặt cầu.

– Nếu d = r, mặt phẳng (P) tiếp xúc với mặt cầu tại một điểm duy nhất.

– Nếu d < r, mặt phẳng (P) cắt mặt cầu theo một đường tròn có bán kính  r'=\sqrt{r^{2}-d^{2}} .  Đặc biệt nếu d = 0 mặt phẳng (P) cắt mặt cầu theo một đường tròn lớn.

2. Ví dụ

Ví dụ 1. Cho hai đường tròn nằm trên hai mặt phẳng khác nhau và có chung một dây cung AB. Chứng minh rằng có một mặt cầu chứa cả hai đường tròn ấy.

Giải

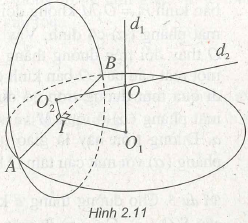
(h.2.11) Gọi O1 và O2 là các tâm của hai đường tròn có chung dây cung là AB và  gọi d1, d2 là các đường thẳng lần lượt . qua O1,  O2 và lần lượt vuông góc với các mặt phẳng chứa các đường tròn đó.

Ta biết rằng d1 chứa tâm các mặt cầu đi qua đường tròn thứ nhất, d2 chứa tâm các mặt cầu đi qua đường tròn thứ hai. Ta chỉ cần chứng minh d1 và d2 cắt nhau tại một điểm o nào đó để suy ra mặt cầu tâm o bán kính OA là mặt cầu chứa cả hai đường tròn cho trước.

Thật vậy, gọi I là trung điểm của dây cung AB thì O1I và O2I đều vuông góc với AB. Vì hai đường tròn nằm trong hai mặt phẳng khác nhau nên ta có AB vuông góc với mặt phẳng (IO1O2). Mặt khác dx và d2 đều vuông góc với AB nên dị và d2 đều nằm trong mặt phẳng (IO1O2). Trong mặt phẳng (IO1O2), d1 và d2 lần lượt vuông góc với hai đường thẳng giao nhau O1I và O2I nên d1 và d2 cắt nhau tại một điểm O. Ta có mặt cầu tâm O là mặt cầu cần tìm.

Ví dụ 2. Cho một đường thẳng a cố định và một điểm M cố định nằm ngoài đường thẳng a. Chứng minh rằng khi điểm o thay đổi trên đường thẳng a, các mặt cầu tâm o bán kính r = OM luôn luôn đi qua một đường tròn cố định.

Giải

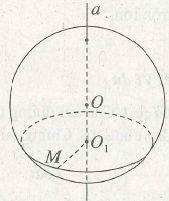
(h.2.12) Gọi (P) là mặt cầu có tâm O thuộc đường thẳng cố định a và đi qua điểm M cố định không thuộc a. Gọi ( α) là mặt phẳng đi qua điểm M và vuông góc với đường thẳng a tại điểm O1 thì O1 cố định và đoạn O1M không đổi. Khi đó mặt phẳng (à) cắt mặt cầu (P) theo đường tròn tâm O1 bán kính O1M. Đường tròn giao tuyến thu được là cố định vì có tâm O1 cố định, bán kính r1 = O1M không đổi và nằm trong mặt phẳng (α) cố định. Vậy với mỗi điểm O thay đổi trên đường thẳng a cố định, có một mặt cầu tâm O bán kính OM luôn luôn đi qua một đường tròn cố định nằm trong mặt phẳng (α) đi qua M và vuông góc với a. Đường tròn này là giao tuyến của mặt phẳng (α) với mặt cầu tâm o bán kính OM.

Ví dụ 3. Cho đường thẳng d không cắt mặt cầu S(O ; r). Gọi (α) là mặt phẳng đi qua tâm o của mặt cầu và vuông góc với đường thẳng d. Xác định giao tuyến của (α) với mặt cầu cho trước và chứng minh rằng có hai mặt phẳng đi qua d và tiếp xúc với mặt cầu.

Giải

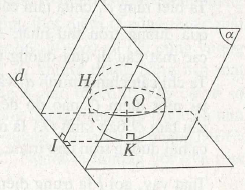
(h.2.13) Gọi (α) là mặt phẳng đi qua tâm o của mặt cầu và vuông góc với đường thẳng d tại I. Mặt phẳng (α) cắt mặt cầu theo đường tròn lớn tâm o có bán kính r và tất nhiên đường tròn này thuộc ( α).

Trong mặt phẳng (α) gọi IH và IK là hai tiếp tuyến của đường tròn lớn đó cùng đi qua điểm I. Khi đó mặt phẳng (d, H) và mặt phẳng (d, K) là hai mặt phẳng đi qua d và tiếp xúc với mặt cầu. Thật vậy ta có OK  ⊥ d vì OK thuộc (α), mặt khác OK ⊥ IK, do đó OK vuông góc với mặt phẳng (d, K) nên mặt phẳng (d, K) tiếp xúc với mặt cầu. Tương tự ta chứng minh mặt phẳng (d, H) tiếp xúc với mặt cầu. Như vậy ta có hai mặt phẳng đi qua d tiếp xúc với mặt cầu S(O ; r) cho trước.

VẤN ĐỀ 3:

Xét vị trí tương đối của một mặt cầu và một đường thẳng

1. Phương pháp giải

Xét khoảng cách d từ tâm O của mặt cầu đến đường thẳng cho trước :

Nếu d <r, đường thẳng cắt mặt cầu tại hai điểm ;

Nếu d = r, đường thẳng tiếp xúc với mặt cầu ;

Nếu d>r, đường thẳng không cắt mặt cầu.

*Có thể sử dụng các kiến thức về hệ thức lượng trong tam giác và hệ thức lượng trong đường tròn trong mặt phẳng để giải toán.

2. Ví dụ

Ví dụ 1. Cho mặt cầu S(O ; r) và một điểm A biết OA = 2r. Qua A kẻ một tiếp tuyến với mặt cầu tại B và kẻ một cát tuyến cắt mặt cầu tại c và D. Cho biết CD= r\sqrt{3} .

a) Tính độ dài đoạn

b) Tính khoảng cách từ o đến đường thẳng

Giải

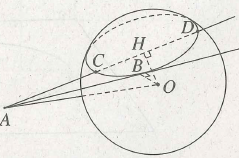
(h.2.14) Ta có AB là tiếp tuyến của mặt cầu tại B nên AB ⊥ OB.

Do đó  AB =\sqrt{OA^{2}-OB^{2}}=\sqrt{4r^{2}-r^{2}}=r\sqrt{3} .

Gọi H là hình chiếu vuông góc của o lên Ta có : oc = OD — r nên tam giác OCD cân tại o và H là trang điểm của đoạn CD, nghĩa là  HC=\frac{CD}{2}=\frac{r\sqrt{3}}{2} .

Vậy khoảng cách từ O đến Cd là độ dài đoạn OH với  OH=\sqrt{OC^{2}-HC^{2}}=\sqrt{r^{2}-(\frac{r\sqrt{3}}{2})^{2}}=\frac{r}{2}

Ví dụ 2. Cho mặt cầu S(O ; r) tiếp xúc với mặt phẳng (P) tại I. Gọi M là một điểm nằm trên mặt cầu nhưng không phải là điểm đối xứng với I qua tâm O. Từ M ta kẻ hai tiếp tuyến của mặt cầu vuông góc với nhau lần lượt cắt mặt phẳng (p) tại A và B. Chứng minh rằng :   AB^{2}=AI^{2}+IB^{2}

Giải

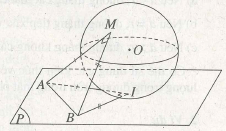
(h.2.15) Vì mặt phẳng (P) tiếp xúc với mặt cầu tại I nên AI và BI là hai tiếp tuyến của mặt cầu tại I . Mặt khác MA và MB là hai tiếp tuyến của mặt cầu tại M.

Như vậy từ một điểm A ngoài mặt cầu ta có hai tiếp tuyến AM và AI nên AM – AI. Lí luận tương tự ta có BM = BI. Ta có hai tam giác ASM và ABI bằng nhau theo trường hợp (c. c. c)     

nên góc AMB = góc AIB = 90°.

Do đó AB^{2}=AI^{2}+IB^{2} (định lí Py-ta-go).

Ví dụ 3. Cho mặt phẳng (α) và hai điểm A, B nằm về một phía của (α) sao cho đường thẳng AB cắt (α) tại I. Tìm tập hợp các tiếp điểm của mặt cầu đi qua B và tiếp xúc với mặt phẳng (α).

Giải

Do đó điểm M nằm trên đường tròn tâm I bán kính  r'=\sqrt{IA.IB}   và đường tròn này nằm trong mặt phẳng ( α).

Ngược lại, lấy điểm M bất kì nằm trên đường tròn đó. Ta gọi o là giao điểm của đường thẳng A vuông góc với mặt phẳng (à) tại M và mặt phẳng trung trực của đoạn AB. Do đó mặt cầu tâm O bán kính OM đi qua B và tiếp xúc với mặt phẳng (à) tại M. Vì IA.IB = IM^{2}   nên mặt cầu đó cũng đi qua A.

VẤN ĐỀ 4:

Mặt cầu ngoại tiếp hình chóp và hình lăng trụ

1. Phương pháp giải

Muốn chứng minh mặt cầu ngoại tiếp một hình chóp hoặc một hình lăng trụ ta cần chứng minh mặt cầu đó ‘đi qua tất cả các đỉnh của hình chóp, hoặc của hình lăng trụ. Sau đó cần xác định tâm và bán kính của mặt cầu ngoại tiếp. Chú ý rằng điều kiện cần và đủ để một hình chóp có mặt cầu ngoại tiếp là đáy của hình chóp đó có đường tròn , ngoại tiếp ; điều kiện cần và đủ để một hình lăng trụ có mặt cầu ngoại tiếp là hình lăng trụ đó phải là một hình lăng trụ đứng và có đáy là một. đa giác có đường tròn ngoại tiếp.

2. Ví dụ

‘Víẩụ 1. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AA’ = a, AB = b, AD = c.

Hãy xác định tâm và bán kính của mặt

cầu đi qua 8 đỉnh của hình hộp đó.                                   B

Tính bán kính của đường tròn là giao tuyến của mặt phẳng (ABCD) với mặt cầu trên.

Giải

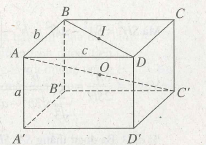
Giả sử hình hộp chữ nhật ABCD.A’B’C’D’ có AB = b, AD = c,  AA’ = a. Ta biết rằng các đường chéo của hình hộp chữ nhật có độ dài bằng nhau và cắt nhau tại trung điểm o của mỗi đường.

a) Ta có OA = OB = OC = OD = OA’ = OB’ – OC’ = OD’ và OA =  AC’/2  bên cạnh đó   AC'=\sqrt{a^{2}+b^{2}+c^{2}} nên  r=AO=\frac{1}{2}\sqrt{a^{2}+b^{2}+c^{2}} .

b) Giao tuyến của (ABCD) với mặt cầu trên là đường tròn ngoại tiếp hình chữ nhật ABCD. Vậy đường tròn giao tuyến của (ABCD) với mặt cầu trên có tâm là trung điểm I của BD và có bán kính  r'=\frac{1}{2}\sqrt{b^{2}+c^{2}} .

 

Đang tải...

Bài mới

loading...

Trackbacks

  1. Mặt cầu - Các kiến thức cần nhớ - Sách bài tập hình học 12 | Học Online

Bình luận

© Hoc360.net. All rights reserved.

Chính sách bảo mật. Quy định sử dụng . Liên hệ .

Email: hoc360net@gmail.com

Mobile: 09026788686

Địa chỉ: Số nhà 20 ngõ 140 Tôn Thất Tùng, Phường Khương Thượng, Quận Đống Đa, Thành phố Hà Nội