Các dạng toán cơ bản về mặt tròn xoay
VẤN ĐỀ 1
Chứng minh đường thẳng d luôn luôn thuộc một mặt nón hay mặt trụ tròn xoay xác định
1. Phương pháp giải
Cần khai thác các tính chất của đường thẳng d qua các giả thiết của bài toán để đưa về kết luận d có thể thuộc mặt nón tròn xoay hoặc thuộc mặt trụ tròn xoay.
2. Ví dụ
Ví dụ 1. Cho hai điểm A, B cố định. Một đường thẳng d di động luôn luôn đi qua A và cách B một đoạn không đổi a = AB/2. Chứng minh rằng d luôn luôn nằm trên một mặt nón tròn xoay.
Giải
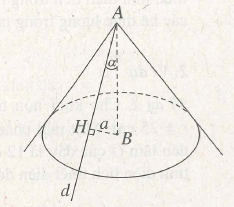
(h.2.1) Ta hãy xét một vị trí tuỳ ý của đường thẳng d đi qua điểm A. Trong mặt phẳng (d, AB) kẻ BH ⊥ d tại H và gọi α = HÂB.
Ta có sin a = BH/AB = a/AB = 1/2 => α =
Vậy α không đổi, suy ra d nằm trên mặt nón đỉnh A, nhận AB làm trục và có góc ở đỉnh bằng 2α = .
Ví dụ 2. Trong mặt phẳng (P) cho đường tròn tâm O, bán kính r = 6 cm. Qua điểm M bất kì nằm trên đường tròn, ta kẻ đường thẳng m vuông góc với (P). Chứng minh rằng đường thẳng m nằm trên một mặt trụ tròn xoay xác định.
Giải
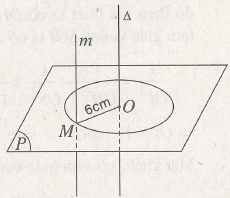
(h.2.2) Gọi Δ là đường thẳng vuông góc với mặt phẳng (P) tại o. Vì m ⊥ (P) nên m // Δ. Đường thẳng m luôn luôn cách đường thẳng Δ cố định một khoảng OM = 6 cm. Vậy đường thẳng m nằm trên mặt trụ tròn xoay nhận Δ làm trục và có bán kính r = 6 cm.
Xem thêm: Câu hỏi & bài tập mặt tròn xoay tại đây.
VẤN ĐỀ 2
Giải các bài toán tìm thiết diện của một mặt phẳng với khối nón. Tính diện tích xung quanh của hình nón và thể tích của khối nón
1. Phương pháp giải
Sử dụng giả thiết và các tính chất của thiết diện tạo bởi mặt phẳng với hình nón (khối nón) để tính diện tích thiết diện, diện tích xung quanh, thể tích của khối nón. Sau khi xác định được các yếu tố có liên quan đến thiết diện, diện tích xung quanh hoặc thể tích của khối nón, cần khéo léo sử dụng các công thức tính diện tích trong hình học phầng và tìm độ dài các đoạn thẳng dựa vào các hệ thức lượng trong tam giác.
2. Ví dụ
Ví dụ 1. Cho khối nón tròn xoay có đường cao h = 20 cm, bán kính đáy r = 25 cm. Một mặt phẳng (P) đi qua đỉnh của khối nón và có khoảng cách đến tâm O của đáy là 12 cm. Hãy xác định thiết diện của (P) với khối nón và tính diện tích thiết diện đó.
Giải
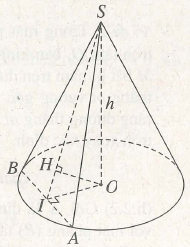
(h.2.3) Gọi S là đỉnh của khối nón. Mặt phẳng (P) đi qua đỉnh S cắt khối nón theo hai đường sinh bằng nhau là SA = SB nên ta có thiết diện là tam giác cân SAB.
Gọi I là trung điểm của đoạn AB, ta có OI ⊥ AB.
Từ tâm O của đáy ta kẻ OH ⊥ SI tại H, ta có OH ⊥ (SAB) và do đó theo giả thiết ta có OH =12 cm. Xét tam giác vuông SOI ta có :
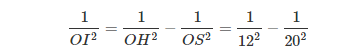
=>OI= 15 (cm).
Mặt khác, xét tam giác vuông SOI ta còn có : OS.OI = SI.OH.
Do đó:
![]()
Gọi St là diện tích thiết diện SAB. Ta có : St = AB.SI, trong đó AB = 2AI.
Vậy thiết diện SAB có diện tích là : St = . 40.25 = 500 (
).
Ví dụ 2. Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Hãy tính diện tích xung quanh và thể tích của khối nón có đỉnh là tâm o của hình vuông ABCD và đáy là hình tròn nội tiếp hình vuông A ‘B’C’D
Giải
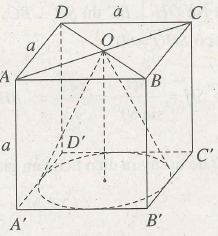
(h.2.4) Khối nón có chiều cao bằng a và có bán kính đáy r = .
Do đó diện tích xung quanh của khối nón được tính theo công thức :
Sxq = πrl trong đó:
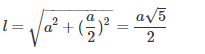
Vậy:
![]()
Thể tích của khối nón được tính theo công thức :
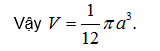
VẤN ĐỀ 3
Cho các yếu tố để xác định mặt trụ tròn xoaỵ hoặc khối trụ tròn xoay hoặc hình trụ tròn xoaỵ. Giải các bài toán tìm thiết diện của một mặt phẳng với khối trụ, tính diện tích xung quanh của hình trụ và tính thể tích của khối trụ
1. Phương pháp giải
Sử dụng giả thiết và các tính chất của thiết diện tạo bởi mặt phẳng với hình trụ (khối trụ) để tính diện tích của thiết diện, diện tích xung quanh, thể tích của khối trụ.
2. Ví dụ
Ví dụ 1. Một khối trụ có chiều cao bằng 20 cm và có bán kính đáy bằng 10 cm. Người ta kẻ hai bán kính OA và O’B’ lần lượt nằm trên hai đáy sao cho chúng hợp với nhau một góc bằng . cắt khối trụ bởi một mặt phẳng chứa đường thẳng AB’ và song song với trục của khối trụ đó. Hãy tính diện tích của thiết diện.
Giải:
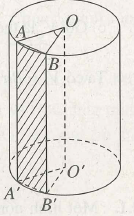
(h.2.6) Từ một đáy của khối trụ ta vẽ hai bán kính
OA, OB sao cho AÔB = . Gọi A’, O’, B’ lần lượt là hình chiếu vuông góc của A, O, B trên mặt đáy còn lại. Ta có OA và O’B’ tạo với nhau một góc
. Thiết diện là hình chữ nhật ABB’A ‘ có :
=
+
–
![]()
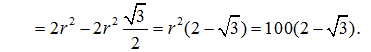
![]()
Mặt khác ta có AA’ = BB’ = OO’ = 20 cm.
Do đó thiết diện là hình chữ nhật ABB’A’ có diện tích là :
![]()
Ví dụ 2. Một khối trụ có bán kính đáy bằng r và có thiết diện qua trục là một hình vuông.
a) Tính diện tích xung quanh của khối trụ đó.
b) Tính thể tích của hình lăng trụ tứ giác đều nội tiếp trong hình trụ đã cho (hình lăng trụ này có đáy là hình vuông nội tiếp trong đường tròn đáy của hình trụ).
c) Gọi V là thể tích hình lăng trụ đều nội tiếp trong hình trụ và V’ là thể tích
Giải
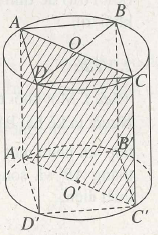
(h.2.7)
Vì thiết diện qua trục hình trụ là một hình vuông nên đường sinh l bằng đường cao h và bằng 2
Do đó diện tích xung quanh của khối trụ đó là :
![]()
Gọi A’B’C’D’ là lăng trụ tứ giác đều nội tiếp trong hình trụ đã cho. Ta có hình vuông ABCD nội tiếp trong đường tròn đáy.
Do đó AB = và ta tính được thể tích của hình lăng trụ tứ giác đều nội tiếp trong hình trụ đã cho là :
![]()
Gọi V’ là thể tích khối trụ có bán kính đáy bằng r và có chiều cao bằng 2r.
Ta có:
![]()
Vậy:

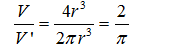



Comments mới nhất