Giá trị lượng giác của một cung – Chương VI: Cung và góc lượng giác. Công thức lượng giác – Giải bài tập đại số 10

Giá trị lượng giác của một cung. Đại 10

A. KIẾN THỨC CƠ BẢN

1. Giá trị lượng giác của cung α

a) Định nghĩa

Trên đường tròn lượng giác cho cung AM có sđ bằng α:

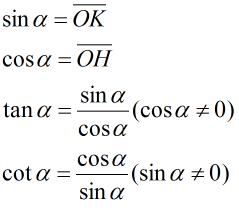
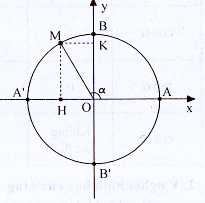
Các giá trị sinα, cosα, tanα, cotα được gọi là các giá trị lượng giác của cung α.

Ta cũng gọi trục tung là trục sin, còn trục hoành là trục coooossin.

b) Hệ quả

* sin(α + k2π) = sinα, ∀k ∈ Z;

* cos(α + k2π) = cosα, ∀k ∈ Z;

* -1 ≤ sinα ≤ 1

* -1 ≤ cosα ≤ 1

* tanα xác định với mọi 

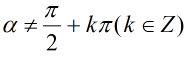
* cotα xác định với mọi 

* Với mọi m ∈ R mà -1 ≤ m ≤ 1 đều tồn tại α và β sao cho sinα = m và cosβ = m.

* Dấu của các giá trị lượng giác của góc α phụ thuộc vào vị trí điểm cuối của cung AM bằng α trên đường tròn lượng giác.

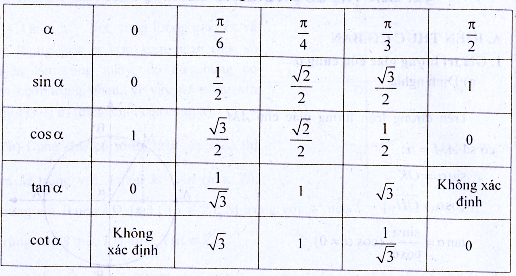
c) Giá trị lượng giác của các cung đặc biệt

2. Ý nghĩa hình học của tang (tan) và côtang (cot)

a) Ý nghĩa hình học của tanα

tanα được biểu diễn bởi độ dài đại số của vecto AT trên trục t’At. Trục t’At được gọi là trục tang. (tham khảo hình 50 trang 144 SGK)

tanα = AT¯

b) Ý nghĩa hình học của cotα

cotα được biểu diễn bởi độ dài đại số của vecto BS trên trục s’BS. Trục s’Bs được gọi là trục côtang. (tham khảo hình 51 trang 144 SGK)

cotα = BS¯

3. Quan hệ giữa các giá trị lượng giác

a) Công thức lượng giác cơ bản

c) Giá trị lượng giác của các cung có liên quan đặc biệt

– Cung đối nhau: α và -α

cos (-α) = -cosα

sin (-α) = -sinα

tan (-α) = -tanα

cot (-α) = -cotα

– Cung bù nhau: α và π – α

sin(π – α) = sinα

cos(π – α) = -cosα

tan(π – α) = -tanα

cot(π – α) = -cotα

– Cung hơn kém π; α và (π + α)

sin(α + π) = -sinα

cos(α + π) = -cosα

tan(α + π) = tanα

cot(α + π) = cotα

– Cung phụ nhau: α và (π/2 – α)

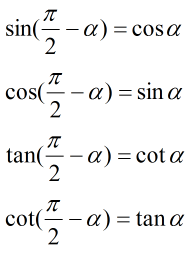
B. HƯỚNG DẪN GIẢI BÀI TẬP (SGK)

Bài 1 (Trang 148, SGK)

Vì sinα có tập giá trị là đoạn [-1;1] và vì: -1 < -0,7 < 1; 4/3 > 1; – < -1; /2 > 1 nên tồn tại cung α mà sinα = -0,7 và không tồn tại α mà sinα nhận một trong các giá trị còn lại.

Bài 2 (Trang 148, SGK)

a) Không, vì không thỏa mãn: α + α = 1.

b) Có, vì:

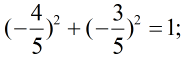
c) Không, vì  ≠ 1.

Bài 3 (Trang 148, SGK)

a) Ta có:

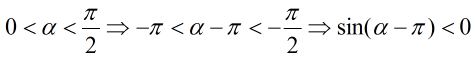
b) Ta có:

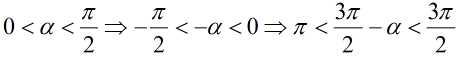
suy ra điểm cuối của cung 3π/2 – α thuộc cung (III) do đó cos(3π/2 – α) < 0.

c) Ta có:

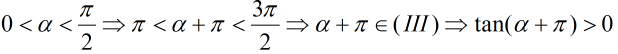
d) Ta có:

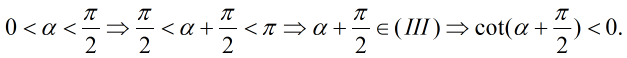
Bài 4 (Trang 148, SGK)

a) 0 < α < π/2 ⇒ sinα > 0.

Áp dụng công thức:

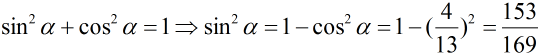
Vậy:

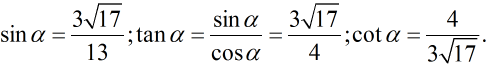
b) π < α < 3π/2 ⇒ cosα < 0.

Áp dụng công thức: α + α = 1

⇒ α = 1 – α = 1 – = 0,51 ⇒ cosα ≈ -0,71

Vậy:

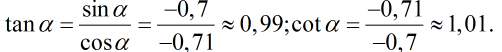
c) π/2 < α < π ⇒ sinα < 0, cosα > 0.

Áp dụng công thức:

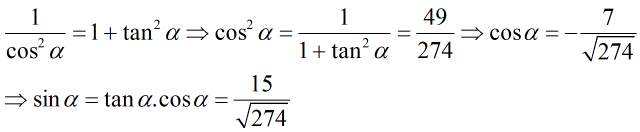
Vậy cotα = -7/15.

d) 3π/2 < α < 2π ⇒ sinα < 0, cosα > 0

Áp dụng công thức:

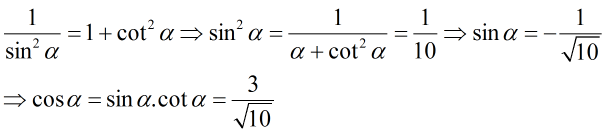
Vậy tanα = -1/3.

Bài 5 (Trang 148, SGK)

a) cosα = 1 ⇒ α = k2π (k ∈ Z)

b) cosα = -1 ⇒ α = π + k2π ( k ∈ Z)

c) cosα = 0 ⇒ α = π/2 + kπ ( k ∈ Z)

d) sinα = 1 ⇒ α = π/2 + k2π ( k ∈ Z)

e) sinα = -1 ⇒ α = -π/2 + k2π ( k ∈ Z)

f) sinα = 0 ⇒ α = kπ ( k ∈ Z).