Chuyên đề: Cấp số cộng
A. LÝ THUYẾT
I, ĐỊNH NGHĨA.
Cấp số cộng là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi .
Số không đổi d được gọi là công sai của cấp số cộng.
Đặc biệt, khi d = 0 thì cấp số cộng là một dãy số không đổi (tất cả các số hạng đều bằng nhau).
Nhận xét: Từ định nghĩa, ta có:
1) Nếu () là một cấp số cộng với công sai , ta có công thức truy hồi
=
+ d,
(1)
2) Cấp số cộng () là một dãy số tăng khi và chỉ khi công sai d > 0.
3) Cấp số cộng () là một dãy số giảm khi và chỉ khi công sai d < 0.
STUDY TIP
Để chứng minh dãy số là một cấp số cộng, chúng ta cần chứng minh
–
là một hằng số với mọi số nguyên dương n.
II, SỐ HẠNG TỔNG QUÁT CỦA CẤP SỐ CỘNG.
Định lý 1.
Nếu cấp số cộng có số hạng đầu
và công sai d thì số hạng tổng quát
được xác định bởi công thức:
![]()
STUDY TIP
Từ kết quả của định lý 1, ta rút ra nhận xét sau:
Cho cấp số cộng () biết hai số hạng $latex u_{p} $ và
thì số hạng đầu và công sai được tính theo công thức:
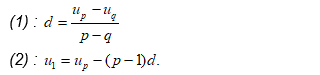
III, TÍNH CHẤT CÁC SỐ HẠNG CỦA CẤP SỐ CỘNG.
Định lý 2.
Trong một cấp số cộng (), mỗi số hạng (trừ số hạng đầu và cuối) đều là trung bình cộng của hai số hạng đứng kề với nó, nghĩa là
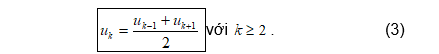
STUDY TIP
Một cách tổng quát, ta có:
![]()
IV, TỔNG n SỐ HẠNG ĐẦU TIÊN CỦA CẤP SỐ CỘNG.
Định lý 3.
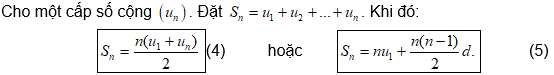
STUDY TIP
1) Chúng ta thường sử dụng công thức (4) để tính khi biết số hạng đầu và số hạng thứ n của cấp số cộng.
2) Để tính được , thì công thức (5) được sử dụng mọi trường hợp. Cụ thể là, chúng ta cần tìm được số hạng đầu
và công sai d của cấp số cộng.
3) Các bài toán về cấp số cộng thường đề cập đến 5 đại lượng , d, n,
,
. Chúng ta cần biết ba đại lượng trong năm đại lượng là có thể tìm được hai đại lượng còn lại. Tuy nhiên, theo các công thức tính
,
thì các bài toán về cấp số cộng sẽ quy về việc tính ba đại lượng
, d, n.
B. CÁC DẠNG TOÁN VỀ CẤP SỐ CỘNG
Dạng 1: Bài tập nhận dạng cấp số cộng
Dạng 2: Bài tập về xác định số hạng và công sai của cấp số cộng.
Dạng 3: Bài tập về tổng của N số hạng đầu tiên của cấp số cộng.
Dạng 4: Bài tập liên quan đến tính chất của cấp số cộng.
Dạng 5: Bài tập liên quan đến cấp số cộng.




Comments mới nhất