Đáp án Bài tập ôn chương III - Sách Bài tập Toán 9 Tập 2 phần Hình học

Đang tải...

Đáp án Bài tập ôn chương III

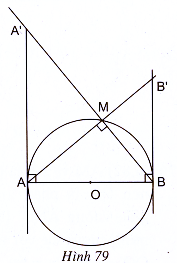73. (h.79) a) Từ hai tam giác vuông đồng dạng ΔAA’B ∼ ΔBAB’, ta có

b) Từ hai tam giác vuông đồng dạng ΔA’MA ∼ ΔA’AB, ta có

74. (h.80)

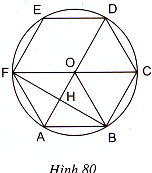Vẽ lục giác đều ABCDEF cùng với đường tròn ngoại tiếp. Dễ thấy rằng DA là đường kính và tứ giác OFAB là hình thoi. Gọi giao điểm của AD và BF là H. Ta có :

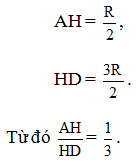
75. (h.81) Giả sử M là điểm nằm trong tam giác ABC sao cho $\widehat{AMB}$ = $\widehat{BMC}$ = $\widehat{CMA}$ thế thì điểm M nhìn các cạnh AB, BC, CA của tam giác ABC dưới cùng một góc là 120°. Suy ra cách dựng sau :

Dựng cung tròn chứa góc 120° vẽ trên đoạn thẳng BC.

Dựng cung tròn chứa góc 120° vẽ trên đoạn thẳng AC.

Giao điểm của hai cung tròn này là điểm M phải dựng.

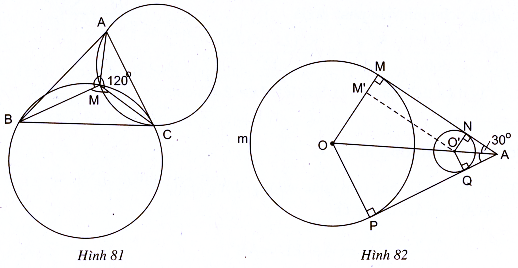
76. (h.82) AM và AP là hai tiếp tuyến chung xuất phát từ A đến đường tròn (O) nên OA là phân giác của MAP. Vì $\widehat{MAP}$ = 60° nên $\widehat{MAO}$ = 30°. Tam giác vuông ANO’ là nửa tam giác đều, ta có O’A = 2O’N = 2a. Chứng minh tương tự với tam giác vuông AMO, ta có OA = 2OM = 8a, từ đó OO’ = 8a – 2a = 6a.

Từ O’ kẻ OM’ // NM (M’ nằm trên bán kính OM) ta có M’O’ = MN (vì MNO’M’ là hình chữ nhật). Áp dụng định lí Py-ta-go vào tam giác vuông OM’O’ ta có

Suy ra MN = 3a $\sqrt3$ .

Tứ giác ANO’Q có $\widehat{N}$ = $\widehat{Q}$ = 90°, $\widehat{A}$ = 60°, suy ra $\widehat{NO'Q}$ = 120°.

Tương tự, ta có $\widehat{MOP}$ = 120°, suy ra cung lớn MmP có

sđ $\widehat{MmP}$ = 360° – 120° = 240°.

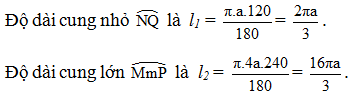
Độ dài của dây cua-roa mắc qua hai ròng rọc là

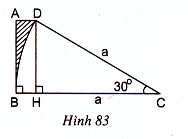77. Diện tích phần gạch sọc trên hình 83 là hiệu giữa diện tích hình thang vuông ABCD

và diện tích hình quạt tròn 30° của đường tròn bán kính

Từ D kẻ DH vuông góc với BG thì tam giác vuông CHD là nửa tam giác đều, ta có

(vì tứ giác ABHD là hình chữ nhật).

Diện tích hình thang vuông ABCD bằng

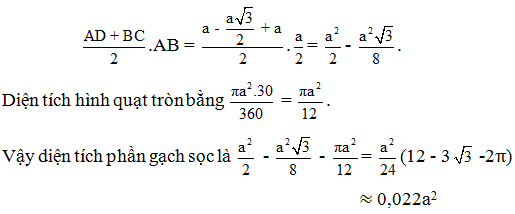
Có thể tính cách khác, như sau :

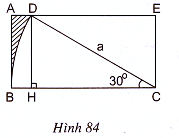Diện tích phần gạch sọc trên hình 84 bằng diện tích hình chữ nhật ABCE trừ đi tổng diện tích hình quạt tròn CBD và tam giác vuông CEĐ.

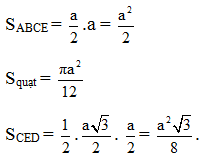
Diện tích phần gạch sọc bằng

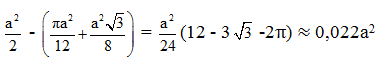
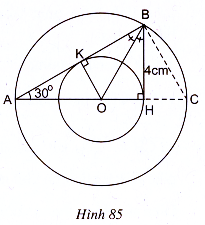78. (h.85) a) Hạ OK vuông góc với AB. Tâm O nằm trên tia phân giác của góc B nên cách đều hai cạnh của góc, ta có OK = OH. Do đó đường tròn (O ; OH) tiếp xúc với cạnh AB.

b) Tia đối của tia HA cắt đường tròn lớn tại C. Nối B với C. Ta có tam giác AOB cân (vì A = ABO = 30°) nên OA = OB. Vậy đường tròn (O ; OA) đi qua B.

$\widehat{ABC}$ = 90° vì là góc nội tiếp chắn nửa đường tròn (O ; OA).

Trong tam giác vuông ABC, ta có

AH.HC = $BH^2$ ,

hay (OA + OH)(OA – OH) = $4^2$

$OA^2$ – $OH^2$ = 16.

Nhân hai vế của (*) với $\pi$ ta có

$\pi$ .( $OA^2$ – $OH^2$ ) = 16 $\pi$ .

Nhưng $\pi$ ( $OA^2$ – $OH^2$ ) chính là diện tích hình vành khăn. Vậy diện tích hình vành khăn nằm giữa hai đường tròn là 16 $\pi$ ( $cm^2$ ).

79. a) (h.86)

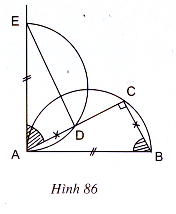• Phần thuận

Nối D với E.

ΔADE = ΔBCA vì chúng có :

AE = AB,

AD = BC,

$\widehat{EAD}$ = $\widehat{ABC}$ (góc có cạnh tương ứng vuông góc).

Khi C di chuyển trên nửa đường tròn đường kính AB, điểm D luôn nhìn đoạn thẳng AE dưới một góc bằng 90°, nên D nằm trên nửa đường tròn đường kính AE.

• Phần đảo

Lấy điểm D’ bất kì trên đường tròn đường kính AE. Đường thẳng AD’ cắt đường tròn đường kính AB tại C’. Nối C’ với B, nối D’ với E. Hai tam giác AD’E và BCA có $\widehat{D'}$ = $\widehat{C'}$ = 90°, AE = AB, $\widehat{EAD'}$ = $\widehat{ABC'}$ (góc có cạnh tương ứng vuông góc) suy ra ΔAD’E = ΔBCA, từ đó AD’ = BC’, đó là điều phải chứng minh.

• Kết luận.

Vậy khi điểm C chạy trên nửa đường tròn đường kính AB thì quỹ tích điểm D là nửa đường tròn đường kính AE. (Khi C trùng với B thì D trùng với A, khi C trùng với A thì D trùng với E).

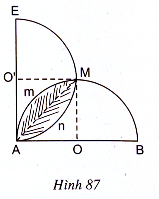
b) (h.87) Gọi tâm của hai nửa đường tròn đường kính AB và AE lần lượt là O và O’. Hai nửa đường tròn này cắt nhau tại điểm thứ hai M. Dễ dàng chứng minh được O’AOM là hình vuông.

Diện tích phần chung của hai nửa đường tròn (O) và (O’) là hai hình viên phân bằng nhau AmM và AnM.

Bài tập bổ sung

III. 1. Xem hình vẽ (h.bs.28).

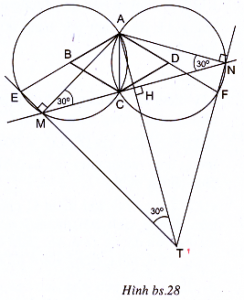a) Ta có $\widehat{AMC}$ = 30° và $\widehat{ANC}$ = 30° (vì cùng chắn cung AC),

suy ra $\widehat{TMC}$ = 60° và $\widehat{TNC}$ = 60°.

Từ đó MNT là tam giác đều.

b) Theo trên MAN là tam giác cân nên AH vuông góc với MN, đồng thời HM = HN.

Khi đó TH cũng vuông góc với MN, suy ra $\widehat{HTM}$ = 30°.

Trong tam giác vuông AHM có

$\widehat{AMH}$ = 30° nên AM = 2 AH.

Trong tam giác vuông AMT có

$\widehat{ATM}$ = 30° nên AT = 2 MA. Suy ra AT = 4 AH.

III. 2. Xem hình vẽ (h.bs.29).

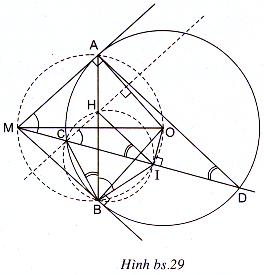Các điểm A, I, B cùng nhìn đoạn MO dưới một góc vuông, do đó cùng thuộc đường tròn đường kính MO.

Do đó $\widehat{AMI}$ = $\widehat{ABI}$ (cùng chắn cung nhỏ AI).

Vì CH và MA cùng vuông góc với OA nên CH // MA, suy ra $\widehat{AMI}$ = $\widehat{HCI}$ (đồng vị). Từ đó, $\widehat{HCI}$ = $\widehat{HBI}$ nên CHIB là tứ giác nội tiếp.