Vị trí tương đối của đường thẳng và đường tròn
Kiến thức cần nhớ:
1) Ba vị trí tương đối
Cho đường tròn (O ; R) và đường thẳng a với d là khoảng cách từ o đến a.
a) d < R <=> a cắt (O);
b) d = R <=> a tiếp xúc với (O);
c) d > R <=> a và (O) không giao nhau.
2) Tiếp tuyến của một đường tròn
Định nghĩa.
Một đường thẳng được gọi là tiếp tuyến của một đường tròn nếu nó chỉ có một điểm chung với đường tròn đó. Điểm chung gọi là tiếp điểm.
Định lí 1.
Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
Đảo lại, nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm ấy thì đường thẳng đó là tiếp tuyến của đường tròn.
Định lí 2.
Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì giao điểm này cách đều hai tiếp điểm, tia kẻ từ giao điểm đó và đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến, tia kẻ từ tâm và đi qua giao điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.
3) Đường tròn nội tiếp
Đường tròn tiếp xúc với ba cạnh của một tam giác gọi là đường tròn nội tiếp tam giác và tam giác đó gọi là tam giác ngoại tiếp đường tròn.
Tâm của đường tròn nội tiếp là giao điểm của ba đường phân giác trong của tam giác.
4) Đường tròn bàng tiếp
Đường tròn tiếp xúc với cạnh BC của tam giác ABC và tiếp xúc với phần kéo dài của hai cạnh AB và AC gọi là đường tròn bàng tiếp trong góc A.
Tâm của đường tròn này là giao điểm của đường phân giác góc A và đường phân giác của góc ngoài B (hoặc giao điểm của hai đường phân giác của hai góc ngoài B và C).
Ví dụ 12
Cho một đoạn thẳng AB và các đường thẳng xx’, yy’ vuông góc với AB tại A và B; một gốc vuông có đỉnh là trung điểm O của AB, một cạnh cắt xx’ tại c, một cạnh cắt yy’ tại D. Chứng minh rằng CD là tiếp tuyến của đường tròn đường kính AB.
Giải
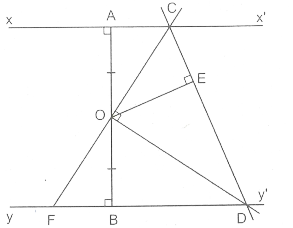
Kẻ OE ⊥ CD. Tia đối của tia OC cắt yy’ tại F. Hai tam giác vuông OAC và OBF bằng nhau (g.c.g) vì có góc A = góc B = 1v, OA = OB (giả thiết) và AÔC= BÔF (đối đỉnh). Suy ra OC = OF.
Tam giác CDF có DO vừa là đường cao, vừa là đường trung tuyến nên là tam giác cân. Do đó DO cũng là đường phân giác. Suy ra OE = OB. Vì vậy, đường tròn tâm O bán kính OB cũng đi qua E và đường thẳng CD vuông góc với bán kính OE tại E nên CD là tiếp tuyến của đường tròn này.
Ví dụ 13
Từ một điểm A ở ngoài đường (O), ta kẻ hai tiếp tuyến AB và AC với đường tròn (B và C là các tiếp điểm). Gọi M là một điểm bất kì trên đường thẳng đi qua các trung điểm của AB và AC. Kẻ tiếp tuyến MK của đường tròn (O). Chứng minh rằng MK = MA.
Giải.
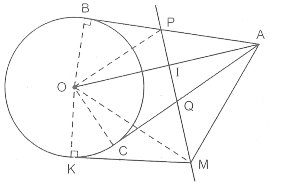
Gọi bán kính của đường tròn (O) là R, các trung điểm của AB và AC là p
và Q, giao điểm của OA và PQ là I. Vì AB và AC là hai tiếp tuyến của đường
tròn (O) cắt nhau tại A nên AB = AC và AO là tia phân giác của BÂC .
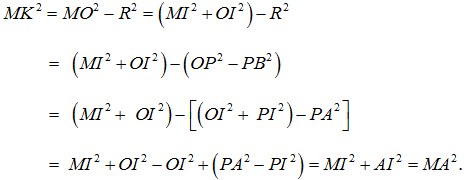
Vậy MK = MA.
Ví dụ 14
Trong tam giác ABC, a, b, c là độ dài các cạnh BC, AC, AB ; 2p là chu vi; S là diện tích ; r, 
a) Chứng minh AE’ = AF’ = p.
b) Chứng minh AE = AF = p – a.
c) Chứng minh S = pr = (p – a)
d) Từ các kết quả trên, hãy chứng minh rằng
S = 
Giải
a)
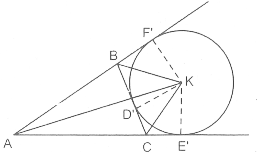
Đường tròn bàng tiếp trong góc A tiếp xúc với BC, AC, AB tại D’, E’ và F. Ta có :
AE’ = AF, BD’ = BF, CD’ = CE’ (hai tiếp tuyến của một đường tròn cùng xuất phát từ một điểm). Suy ra AE’ + AF’ = (AC + CD’) + (AB + BD’) = AC + BC + + AB = 2p.
Do đó : AE’ = AF’ = p.
b)
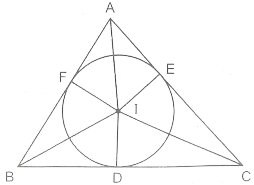
Dễ thấy AE = AF, BD = BF, CD = CE
Suy ra AE + a = AE + BD + CD = p.
Do đó : AE = AF = p – a.
Tương tự, ta cũng có BD = BF = p – b, CD = CE = p – c.
c) Gọi I là tâm đường tròn nội tiếp tam giác ABC, K là tâm đường tròn bàng tiếp trong góc A.
Ta có
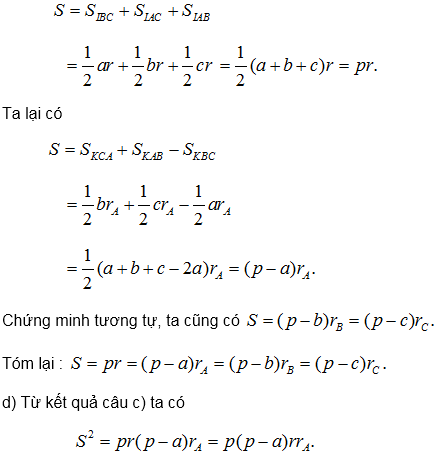
Ghi chú.
Công thức S =
BÀI TẬP
40. Cho một điểm A ở ngoài đường tròn (O). Kẻ hai cát tuyến AMN và APQ tới đường tròn sao cho MN > PQ. Dựng đường tròn (O ; OA). Kẻ hai dây AD và AF của đường tròn lớn tiếp xúc với đường tròn nhỏ tại B và c. Cát tuyến AMN và cát tuyến APQ cắt đường tròn lớn ở E và H.
a) Chứng minh AD = AF.
b) Chứng minh AE > AH.
c) Chứng minh bốn điểm A, B, O, C cùng nằm trên một đường tròn.
d) So sánh OÂE và OÂH .
41. Cho đường tròn (O) và một điểm A nằm cùng một phía đối với đường thẳng xy cho trước (A ở ngoài (O)). Hãy tìm một điểm p trên xy sao cho nếu từ p vẽ tiếp tuyến PB với đường tròn (O) thì PB và PA tạo với xy những góc bằng nhau.
42. Cho một điểm p ở ngoài đường tròn (O). Đường thẳng PO cắt đường tròn tại A và B (A nằm giữa o và P). Chứng minh rằng PA là khoảng cách nhỏ nhất và PB là khoảng cách lớn nhất trong các khoảng cách từ p đến mọi điểm của đường tròn (O).
43. Trên tiếp tuyến tại A của đường tròn (O), ta lấy hai điểm B và C. Kẻ các tiếp tuyến BD và CE của đường tròn (O). Chứng minh rằng các góc BOC và DAE bằng nhau hoặc bù nhau.
44. Gọi C là một điểm bất kì trên nửa đường tròn đường kính AB tâm O. Tiếp tuyến tại C cắt đường thẳng AB tại D. Từ O kẻ một tia vuông góc với tia phân giác của góc CDO tại E và cắt tiếp tuyến DC tại M. Tìm tập hợp các điểm M.
45. Cho một điểm A trên cạnh Ox của góc xOy. Vẽ đường tròn tiếp xúc với Ox ở A và tiếp xúc với Oy ở B. Tìm tập hợp các điểm B khi cạnh Oy quay quanh đỉnh O.
46. Cho đường thẳng xy ở ngoài đường tròn (O). Hãy dựng cát tuyến ABC vuông góc với xy (A trên xy, B và c trên (O)) sao cho B là trung điểm của AC.
47. Cho hai điểm A, B ở ngoài đường tròn (O). Hãy dựng đường kính COD của đường tròn (O) sao cho AC = BD.
48*. Cho tứ giác ABCD có đường tròn đường kính AB tiếp xúc với đường thẳng CD. Chứng minh rằng đường tròn đường kính CD tiếp xúc với đường thẳng AB khi và chỉ khi các đường thẳng BC và AD song song.
49*. Qua điểm A nằm trong góc nhọn xMy, hãy dựng một đường tròn tiếp xúc với hai cạnh của góc sao cho đường tròn đó có :
a) Bán kính lớn nhất;
b) Bán kính nhỏ nhất.
50. Cho tam giác nhọn ABC nội tiếp một đường tròn. Các tiếp tuyến của đường tròn tại A và c cắt tiếp tuyến tại B ở M và N. Kẻ đường cao BP của tam giác ABC. Chứng minh rằng tia PB là tia phân giác của góc MPN.
51. Trên các cạnh BC và CD của hình vuông ABCD, lấy các điểm M và N sao cho chu vi tam giác MNC bằng nửa chu vi hình vuông. Tìm số đo góc MAN.
52. Cho tam giác ABC có độ dài các đường cao là số nguyên và bán kính của đường tròn nội tiếp tam giác bằng 1 (đơn vị độ dài). Chứng minh rằng ABC là tam giác đều.
53. Dựng tam giác biết một cạnh, chiều cao ứng với cạnh đó và bán kính của đường tròn nội tiếp tam giác.
Comments mới nhất