Tích của vectơ với một số – Sách bài tập toán 10 – Bài tập Hình học

Đang tải...

Tích của vectơ với một số hình học lớp 10

A. CÁC KIẾN THỨC CẦN NHỚ

1. Định nghĩa tích của vectơ với một số. Cho số k và vectơ $\vec{a}$ , dựng được vectơ k $\vec{a}$ .

2. Các tính chất của phép nhân vectơ với một số: Với hai vectơ $\vec{a}$ , $\vec{b}$ tùy ý và với mọi số k, h ∈ $\mathbb{R}$ ta có:

k( $\vec{a}$ + $\vec{b}$ ) = k $\vec{a}$ + k $\vec{b}$ ;
(h + k) $\vec{a}$ = h $\vec{a}$ + k $\vec{a}$ ;
h(k $\vec{a}$ ) = (hk) $\vec{a}$ ;
1. $\vec{a}$ = $\vec{a}$ ; (-1) $\vec{a}$ = – $\vec{a}$ ; 0. $\vec{a}$ = $\vec{0}$ ; k. $\vec{0}$ = $\vec{0}$

3. Hai vectơ $\vec{a}$ , $\vec{b}$ với $\vec{b}$ ≠ $\vec{0}$ cùng phương khi và chỉ khi có số k để $\vec{a}$ = k $\vec{b}$ . Cho hai vectơ $\vec{a}$ và $\vec{b}$ cùng phương $\vec{b}$ ≠ $\vec{0}$ . Ta luôn tìm được số k để $\vec{a}$ = k $\vec{b}$ và khi đó số k tìm được là duy nhất.

4. Áp dụng:

Ba điểm phân biệt A,B,C thẳng hàng ⇔ $\overrightarrow{AB}$ = k $\overrightarrow{AC}$ , với số k xác đinh.
I là trang điểm của đoạn thẳng AB ⇔ $\overrightarrow{MA}$ + $\overrightarrow{MB}$ = 2 $\overrightarrow{MI}$ , ∀M.
G là trọng tâm của tam giác ABC ⇔ $\overrightarrow{MA}$ + $\overrightarrow{MB}$ + $\overrightarrow{MC}$ = 3 $\overrightarrow{MG}$ , ∀M.

5. Cho hai vectơ $\vec{a}$ , $\vec{b}$ ) không cùng phương và $\vec{x}$ là một vectơ tụỳ ý. Bao giờ cũng tìm được cặp số h và k duy nhất sao cho $\vec{x}$ = h $\vec{a}$ + k $\vec{b}$ .

B. DẠNG TOÁN CƠ BẢN

Vấn đề 1.

Xác định vectơ k $\vec{a}$

|k $\vec{a}$ | = |k|| $\vec{a}$ |

Nếu k > 0, k $\vec{a}$ và $\vec{a}$ cùng hướng;

Nếu k < 0, k $\vec{a}$ và $\vec{a}$ ngược hướng.

k. $\vec{0}$ = $\vec{0}$ , 0. $\vec{a}$ , 0. $\vec{0}$ = $\vec{0}$
1. $\vec{a}$ = $\vec{a}$ , (-1) $\vec{a}$ = – $\vec{a}$ .

2. Các ví dụ

Ví dụ 1: Cho $\vec{a}$ = $\overrightarrow{AB}$ và điểm O. Xác định hai điểm M và N sao cho $\overrightarrow{OM}$ = 3 $\vec{a}$ , $\overrightarrow{ON}$ = -4 $\vec{a}$

Giải

Vẽ đường thẳng d đi qua O và song song với giá của $\vec{a}$ . (Nếu O thuộc giá của $\vec{a}$ thì d là giá của $\vec{a}$ ) (h.1.18)

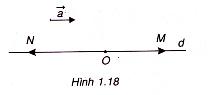
Tích của vectơ với một số hình học lớp 10

Trên d lấy điểm M sao cho OM = 3| $\vec{a}$ |, $\vec{a}$ và $\vec{a}$ cùng hướng khi đó $\vec{OM}$ = 3 $\vec{a}$ . Lấy điểm N trên d sao cho ON = 4| $\vec{a}$ |, $\vec{ON}$ và $\vec{a}$ ngược hướng, khi đó $\vec{ON}$ = -4 $\vec{a}$

Ví dụ 2: Cho đoạn thẳng AB và M là một điểm trên đoạn AB sao cho AM = $\frac15$ AB. Tìm số k trong các đẳng thức sau:

a) $\overrightarrow{AM}$ = k $\overrightarrow{AB}$ ;

b) $\overrightarrow{MA}$ = k $\overrightarrow{MB}$ ;

c) $\overrightarrow{MA}$ = k $\overrightarrow{AB}$

GIẢI

(h.1.19)

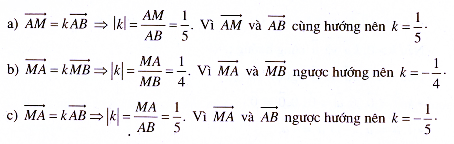
Tích của vectơ với một số hình học lớp 10

Ví dụ 3

a) Chứng minh vectơ đối của vectơ 5 $\vec{a}$ là (-5) $\vec{a}$ .

b) Tìm vectơ đối của các vectơ 2 $\vec{a}$ + 3 $\vec{b}$ , $\vec{a}$ – 2 $\vec{b}$

GIẢI

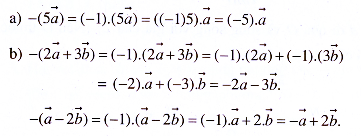
Tích của vectơ với một số hình học lớp 10

Vấn đề 2

Phân tích (biểu thị) một vectơ theo hai vectơ không cùng phương

1. Phương pháp

a) Để phân tích vectơ $\vec{a}$ = $\vec{OC}$ theo hai vectơ không cùng phương $\vec{a}$ = $\vec{OA}$ , $\vec{b}$ = $\vec{OB}$ ta làm như sau:

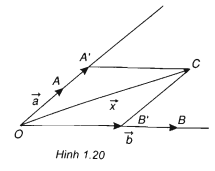Tích của vectơ với một số hình học lớp 10 – Vẽ hình bình hành OA’CB’ có hai đỉnh O, và hai cạnh OA’ và OB’ lần lượt nằm trên hai giá của $\overrightarrow{OA}$ , $\overrightarrow{OB}$ (h.1.20).

Ta có $\overrightarrow{x}$ = $\overrightarrow{OA'}$ + $\overrightarrow{OB'}$

Xác định số h để $\overrightarrow{OA'}$ = h $\overrightarrow{OA}$

Xác định số k để $\overrightarrow{OB'}$ = k $\overrightarrow{OB}$ .

Khi đó $\vec{x}$ = h $\vec{a}$ + k $\vec{b}$ .

b) Có thể sử dụng linh hoạt các công thức sau :

$\overrightarrow{AB}$ = $\overrightarrow{OB}$ – $\overrightarrow{OA}$ , với ba điểm 0,A,B bất kì ;
$\overrightarrow{AC}$ = $\overrightarrow{AB}$ + $\overrightarrow{AD}$ nếu tứ giác ABCD là hình hình hành.

2. Các ví dụ

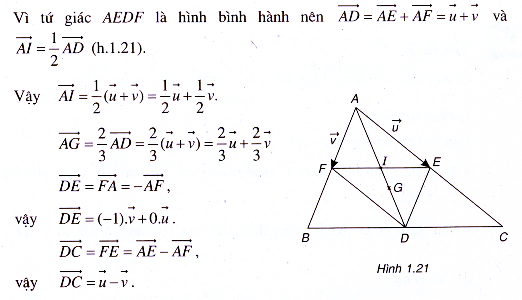
Ví dụ 1. Cho tam giác ABC có trọng tâm G. Cho các điểm D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB và I là giao điểm của AD và EF.

Đặt $\overrightarrow{u}$ = $\overrightarrow{AE}$ , $\overrightarrow{v}$ = $\overrightarrow{AF}$ . Hãy phân tích các vectơ $\overrightarrow{AI}$ , $\overrightarrow{AG}$ , $\overrightarrow{DE}$ , $\overrightarrow{DC}$ theo hai vectơ $\overrightarrow{u}$ , $\overrightarrow{v}$ .

GIẢI

Tích của vectơ với một số hình học lớp 10

Ví dụ 2. Cho tam giác ABC. Điểm M trên cạnh BC sao cho MB = 2MC. Hãy phân tích vectơ $\overrightarrow{AM}$ theo hai vectơ $\overrightarrow{u}$ = $\overrightarrow{AB}$ , $\overrightarrow{v}$ = $\overrightarrow{AC}$ .

GIẢI

Tích của vectơ với một số hình học lớp 10

Vấn đề 3

Chứng minh ba điểm thẳng hàng, hai đường thẳng song song

1. Phương pháp

Dựa vào các khẳng định sau :

Ba điểm phân biệt A, B, cthẳng hàng ⇔ $\overrightarrow{AB}$ và $\overrightarrow{AC}$ cùng phương ⇔ $\overrightarrow{AB}$ = k $\overrightarrow{AC}$ .
Nếu $\overrightarrow{AC}$ = k $\overrightarrow{CD}$ và hai đường thẳng AB và CD phân biệt thì AB // CD.

2. Các ví dụ

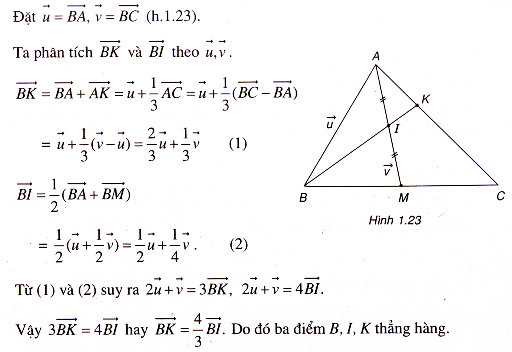
Ví dụ 1. Cho tam giác ABC có trung tuyến AM. Gọi I là trung điểm của AM và K là điểm trên cạnh AC sao cho AK = $\frac13$ AC. Chứng minh ba điểm B, I, K thẳng hàng.

GIẢI

Tích của vectơ với một số hình học lớp 10

Ví dụ 2. Cho tam giác ABC. Hai điểm M, N được xác định bởi các hệ thức : $\overrightarrow{BC}$ + $\overrightarrow{MA}$ = $\overrightarrow{0}$ , $\overrightarrow{AB}$ – $\overrightarrow{NA}$ – 3 $\overrightarrow{AC}$ = $\overrightarrow{0}$ . Chứng minh MN//AC.

GIẢI

Tacó $\overrightarrow{BC}$ + $\overrightarrow{MA}$ + $\overrightarrow{AB}$ – $\overrightarrow{NA}$ – 3 $\overrightarrow{AC}$ = $\overrightarrow{0}$

hay ( $\overrightarrow{AB}$ + $\overrightarrow{BC}$ ) + ( $\overrightarrow{MA}$ + $\overrightarrow{AN}$ ) – 3 $\overrightarrow{AC}$ = $\overrightarrow{0}$

$\overrightarrow{AC}$ + $\overrightarrow{MN}$ – 3 $\overrightarrow{AC}$ = $\overrightarrow{0}$

$\overrightarrow{MN}$ = 2 $\overrightarrow{AC}$

Vậy $\overrightarrow{MN}$ cùng phương vói AC.

Theo giả thiết ta có $\overrightarrow{BC}$ = $\overrightarrow{AM}$ , mà A, B, C không thẳng hàng nên bốn điểm A, B, C, M là một hình bình hành.

Từ đó suy ra M không thuộc đường thẳng AC và MN // AC.

Vấn đề 4

Chứng minh các đẳng thức vectơ có chứa tích của vectơ vói một số

1. Phương pháp

Sử dụng tính chất tích của vectơ với một số.
Sử dụng các tính chất của : ba điểm thảng hàng, trung điểm của một đoạn thẳng, trọng tâm của tam giác.

2. Các ví dụ

Ví dụ 1. Gọi M và N lần lượt là trung điểm của hai đoạn thẳng AB và CD. Chứng minh rằng 2 $\overrightarrow{MN}$ – $\overrightarrow{AC}$ + $\overrightarrow{BD}$ .

GIẢI

Vì N là trung điểm của đoạn thẳng $\overrightarrow{CD}$ nên 2 $\overrightarrow{MN}$ = $\overrightarrow{MC}$ + $\overrightarrow{MD}$ .

Mặt khác $\overrightarrow{MC}$ = $\overrightarrow{MA}$ + $\overrightarrow{AC}$ , $\overrightarrow{MD}$ = $\overrightarrow{MB}$ + $\overrightarrow{BD}$ nên

. $\overrightarrow{MC}$ + $\overrightarrow{MD}$ = $\overrightarrow{MA}$ + $\overrightarrow{AC}$ + $\overrightarrow{MB}$ + $\overrightarrow{BD}$ = $\overrightarrow{AC}$ + $\overrightarrow{BD}$ + ( $\overrightarrow{MA}$ + $\overrightarrow{MB}$ )

= $\overrightarrow{AC}$ + $\overrightarrow{BD}$ (vì M là trung điểm của AB).

Vậy 2 $\overrightarrow{MN}$ = $\overrightarrow{AC}$ + $\overrightarrow{BD}$

Ví dụ 2. Cho hình bình hành ABCD. Chứng minh rằng

$\overrightarrow{AB}$ + 2 $\overrightarrow{AC}$ + $\overrightarrow{AD}$ = 3 $\overrightarrow{AC}$ .

GIẢI

Vì ABCD là hình bình hành nên $\overrightarrow{AB}$ + $\overrightarrow{AD}$ = $\overrightarrow{AC}$ . Do đó

$\overrightarrow{AB}$ + 2 $\overrightarrow{AC}$ + $\overrightarrow{AD}$ = ( $\overrightarrow{AB}$ + $\overrightarrow{AD}$ ) + 2 $\overrightarrow{AC}$ = $\overrightarrow{AC}$ + 2 $\overrightarrow{AC}$ = 3 $\overrightarrow{AC}$ .

Ví dụ 3. Chứng minh rằng nếu G và G’ lần lượt là trọng tâm của hai tam giác ABC và A’B’C’ thì 3 $\overrightarrow{GG'}$ = $\overrightarrow{AA'}$ + $\overrightarrow{BB'}$ + $\overrightarrow{CC'}$ .

GIẢI

Vì G’ là trọng tâm của tam giác A’B’C’ nên

3 $\overrightarrow{GG'}$ = $\overrightarrow{GA'}$ + $\overrightarrow{GB'}$ + $\overrightarrow{GC'}$ . (1)

Hơn nữa $\overrightarrow{GA'}$ = $\overrightarrow{GA}$ + $\overrightarrow{AA'}$

$\overrightarrow{GB'}$ = $\overrightarrow{GB}$ + $\overrightarrow{BB'}$

$\overrightarrow{GC'}$ = $\overrightarrow{GC}$ + $\overrightarrow{CC'}$ .

Cộng từng vế ba đẳng thức trên và vì $\overrightarrow{GA}$ + $\overrightarrow{GB}$ + $\overrightarrow{GC}$ = $\overrightarrow{0}$ nên

$\overrightarrow{GA'}$ + $\overrightarrow{GB'}$ + $\overrightarrow{GC'}$ = $\overrightarrow{AA'}$ + $\overrightarrow{BB'}$ + $\overrightarrow{CC'}$ . (2)

Từ (1) và (2) suy ra 3 $\overrightarrow{GG'}$ – $\overrightarrow{AA'}$ + $\overrightarrow{BB'}$ + $\overrightarrow{CC'}$ .

Có thể chứng minh như sau

Ta có $\overrightarrow{GG'}$ = $\overrightarrow{GA}$ + $\overrightarrow{AA'}$ + $\overrightarrow{A'G'}$

$\overrightarrow{GG'}$ = $\overrightarrow{GB}$ + $\overrightarrow{BB'}$ + $\overrightarrow{B'G'}$

$\overrightarrow{GG'}$ = $\overrightarrow{GC}$ + $\overrightarrow{CC'}$ + $\overrightarrow{C'G'}$ .

Cộng từng vế của ba đẳng thức trên và sử dụng điều kiện của trọng tâm tam giác ta suy ra điều cần chứng minh.

Vấn đề 5.

Xác định vị trí của một điểm nhờ đẳng thức vectơ

1. Phương pháp

Sử dụng các khẳng định và các công thức sau :

$\overrightarrow{AB}$ = $\overrightarrow{0}$ ⇔ A ≡ B ;
Cho điểm A và cho $\overrightarrow{a}$ . Có duy nhất điểm M sao cho $\overrightarrow{am}$ = $\overrightarrow{a}$ ;
$\overrightarrow{AB}$ = $\overrightarrow{AC}$ ⇔ B ≡ C, $\overrightarrow{A_1B}$ = $\overrightarrow{AB}$ ⇔ $A_1$ ≡ A.

2. Các ví dụ

Ví dụ 1. Cho tam giác ABC có D là trung điểm của BC. Xác định vị trí của điểm G biết $\overrightarrow{AG}$ = 2 $\overrightarrow{GD}$ .

GIẢI

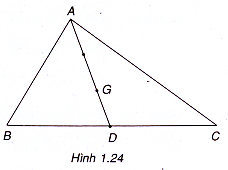
Tích của vectơ với một số hình học lớp 10

Từ $\overrightarrow{AG}$ = 2 $\overrightarrow{GD}$ , suy ra ba điểm A, G, D thẳng hàng, AG = 2GD và điểm G ở giữa A và D. Vậy G là trọng tâm của tam giác ABC (h.1.24).

Ví dụ 2. Cho hai điểm A và B. Tìm điểm I sao cho $\overrightarrow{IA}$ + 2 $\overrightarrow{IB}$ = $\overrightarrow{0}$

GIẢI

$\overrightarrow{IA}$ + 2 $\overrightarrow{IB}$ = $\overrightarrow{0}$ ⇔ $\overrightarrow{IA}$ = -2 $\overrightarrow{IB}$

Từ đó suy ra | $\overrightarrow{IA}$ | = |-2 $\overrightarrow{IB}$ | hay IA = 2IB, $\overrightarrow{IA}$ và $\overrightarrow{IB}$ ngược hướng (h.1.25).

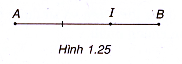
Tích của vectơ với một số hình học lớp 10

Vậy I là điểm thuộc đoạn AB mà IB = $\frac 13$ AB.

Ví dụ 3. Cho tứ giác ABCD. Xác định vị trí điểm G sao cho

$\overrightarrow{GA}$ + $\overrightarrow{GB}$ + $\overrightarrow{GC}$ + $\overrightarrow{GD}$ = $\overrightarrow{0}$ .

GIẢI

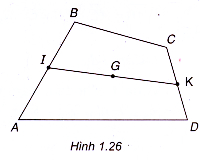
Tích của vectơ với một số hình học lớp 10

Ta có $\overrightarrow{GA}$ + $\overrightarrow{GB}$ = 2 $\overrightarrow{GI}$ , trong đó I là trung điểm của AB và $\overrightarrow{GC}$ + $\overrightarrow{GD}$ = 2 $\overrightarrow{GK}$ , trong đó K là trang điểm của CD. Vậy theo giả thiết ta có 2 $\overrightarrow{GI}$ + 2 $\overrightarrow{GK}$ = $\overrightarrow{0}$ hay $\overrightarrow{GI}$ + $\overrightarrow{GK}$ = $\overrightarrow{0}$ (h. 1.26).

Do đó G là trang điểm của đoạn thẳng IK.

C. CÂU HỎI VÀ BÀI TẬP

1.20. Tìm giá trị của m sao cho $\vec{a}$ = m $\vec{b}$ trong các trường hợp sau :

a) $\vec{a}$ = $\vec{b}$ ≠ $\vec{0}$ ;

b) a = -b và a * 0 ;

c) $\vec{a}$ = – $\vec{b}$ cùng hướng và | $\vec{a}$ | = 20,| $\vec{b}$ | = 5 ;

d) $\vec{a}$ , $\vec{b}$ ngược hướng và | $\vec{a}$ | = 5, | $\vec{b}$ | = 15 ;

e) $\vec{a}$ = $\vec{0}$ , $\vec{b}$ ≠ $\vec{0}$ ;

g) $\vec{a}$ ≠ $\vec{0}$ , $\vec{b}$ = $\vec{a}$ ;

h) $\vec{a}$ = $\vec{0}$ , $\vec{b}$ = $\vec{0}$ .

⇒ Xem đáp án tại đây.

1.21. Chứng minh rằng :

a) Nếu $\vec{a}$ = $\vec{b}$ thì m $\vec{a}$ = m $\vec{b}$ ) ;

b) m $\vec{a}$ = m $\vec{b}$ và m ≠ 0 thì $\vec{a}$ = $\vec{b}$ ;

c) Nếu m $\vec{a}$ = n $\vec{a}$ và $\vec{a}$ ≠ $\vec{0}$ thì m = n

⇒ Xem đáp án tại đây.

1.22. Chứng minh rằng tổng của $\vec{n}$ vectơ $\vec{a}$ bằng n $\vec{a}$ (n là số nguyên dương).

⇒ Xem đáp án tại đây.

1.23. Cho tam giác ABC. Chứng minh rằng nếu $\vec{GA}$ + $\vec{GB}$ + $\vec{GC}$ = $\vec{0}$ thì G là trọng tâm của tam giác ABC.

⇒ Xem đáp án tại đây.

1.24. Cho hai tam giác ABC và A’B’C’. Chứng minh rằng nếu $\vec{AA'}$ + $\vec{BB'}$ + $\vec{CC'}$ = $\vec{0}$ thì hai tam giác đó có cùng trọng tâm.

⇒ Xem đáp án tại đây.

1.25. Cho hai vectơ không cùng phương $\vec{a}$ và $\vec{b}$ . Dựng các vectơ :

⇒ Xem đáp án tại đây.

1.26. Cho lục giác đều ABCDEF tâm O có cạnh a

a) Phân tích vectơ $\vec{AD}$ theo hai vectơ $\vec{AB}$ và $\vec{AF}$

b) Tính độ dài của vectơ $\frac12$ $\vec{AD}$ + $\frac12$ $\vec{BC}$ theo a.

⇒ Xem đáp án tại đây.

1.27. Cho tam giác ABC có trung tuyến $\vec{AM}$ (M là trung điểm của BC). Phân tích vectơ $\vec{AM}$ theo hai vectơ $\vec{AB}$ và $\vec{AC}$ .

⇒ Xem đáp án tại đây.

1.28. Cho tam giác Gọi M là trung điểm của AB và N là một điểm trên cạnh AC sao cho NA = 2NC. Gọi K là trung điểm của MN.

Phân tích vectơ $\vec{AK}$ theo $\vec{AB}$ và $\vec{AC}$ .

⇒ Xem đáp án tại đây.

1.29. Cho tam giác Dựng $\vec{AB'}$ = $\vec{BC}$ , $\vec{CA'}$ = $\vec{AB}$ và $\vec{BC'}$ = $\vec{CA}$ .

a) Chứng minh rằng A là trung điểm của B’C’.

b) Chứng minh các đường thẳng AA’, BB’ và CC’ đồng quy.

⇒ Xem đáp án tại đây.

1.30. Cho tam giác Điểm I trên cạnh AC sao cho CI = $\frac14$ CA, J là điểm mà

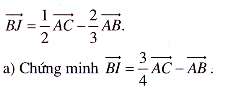
Tích của vectơ với một số hình học lớp 10

b) Chứng minh B, I, J thẳng hàng.

c) Hãy dựng điểm J thoả mãn điều kiện đề bài.

⇒ Xem đáp án tại đây.

1.31. Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Chứng minh rằng vói điểm M bất kì ta có $\vec{MA}$ + $\vec{MB}$ + $\vec{MC}$ + $\vec{MD}$ = 4 $\vec{MO}$ .