Giải bài tập nhân đa thức với đa thức sách giáo khoa Toán lớp 8

Nov 25th, 2017 · 2 Comments
Đang tải...

Giải bài tập nhân đa thức với đa thức sách giáo khoa Toán lớp 8

Kiến thức cần nhớ:

Quy tắc:

Muốn nhân một đa thức với một đa thức , ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau .

Chú ý : 

Tích của hai đa thức là một đa thức .

ĐỀ BÀI :

Bài 7 (tr. 8 SGK)

Làm tính nhân:
a) ({x^2}  – 2x+ 1)(x – 1);                      b) ({x^3} – 2{x^2}  + x -1)(5 – x).

Từ câu b), hãy suy ra kết quả phép nhân: ({x^3} – 2{x^2}  + x -1)(x – 5).

Bài 8 (tr. 8 SGK)

Làm tính nhân:

a) ({x^2}{y^2} - \frac{1}{2}xy + 2y)(x - 2y) ;

b) ({x^2} - xy + {y^2})(x - y) ;

Bài 9 (tr. 8 SGK)

Điền kết quả tính được vào bảng:

Bài 10 (tr. 8 SGK)

Thực  hiện phép tính:

a) ({x^2} - 2x + 3)(\frac{1}{2}x - 5x)

b) ({x^2} - xy + {y^2})(x - y)

Bài 11 (tr. 8 SGK)

Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến:

(x – 5)(2x + 3) – 2x(x – 3) + x + 7.

Bài 12 (tr. 8 SGK)

Tính giá trị biểu thức ({x^2}  – 5)(x + 3) + (x + 4)(x – {x^2} ) trong mỗi trường hợp sau:

a) x = 0;                 b) x = 15;

c) x = -15;               d) x = 0,15.

Bài 13 (tr. 9 SGK)

Tìm x, biết:

(12x – 5)(4x – 1) + (3x – 7)(1 -16x) = 81.

Bài 14 (tr. 9 SGK)

Tìm ba số tự nhiên chẵn liên tiếp, biết tích của hai số sau lớn hơn tích của hai số đầu là 192.

Bài 15 (tr.9 SGK)

Làm tính nhân:

a) ( \frac{1}{2 } x + y)( \frac{1}{2 } x + y);              b) ( x – \frac{1}{2 } y ) ( x – \frac{1}{2 } ) y

Xem thêm :Bài tập phần nhân đơn thức với đa thức 😛

HƯỚNG DẪN – BÀI GIẢI – ĐÁP SỐ

Bài 7 (tr. 8 SGK)

Hướng dẫn:

Áp dụng quy tắc nhân đa thức với đa thức:

(A + B).(C + D) = A.C + A.D + B.C + B.D. Chú ý các phép tính về luỹ thừa:

{a^m}.{a^n} = {a^{m + n}}.   ; {({a^m})^n} = {a^{m.n}} = {a^{m.n}};{a^0} = 1(a \ne 0).

a) Thực hiện phép nhân đa thức với đa thức ta có:

({x^2}  – 2x + 1)(x  – 1)

= {x^3}  – {x^2}  – 2{x^2}  + 2x + x – 1

= {x^3}  –  3{x^2}  + 3x –  1.

b) ({x^3} – 2{x^2}  + x – 1)(5 – x)

= 5{x^3} – {x^4} – 10{x^2} + 2{x^3} + 5x – {x^2} – 5 + x

= – {x^4} + 7{x^3} – 11{x^2} + 6x – 5

Vì x – 5 = -(5 – x) nên:

({x^3}  – 2{x^2}  + x – 1)(x – 5)

=-({x^3}  – 2{x^2} + x – 1)(5 – x)

= {x^4 } – 7{x^3 }  + 11{x^2 }  – 6x + 5.

Bài 8 (tr. 8 SGK)

Giải:

a)

({x^2}{y^2} - \frac{1}{2}xy + 2y)(x - 2y) = {x^3}{y^2} - 2{x^2}{y^3} - \frac{1}{2}{x^2}y + x{y^2} + 2xy - 4{y^2}

b)

({x^2} - xy + {y^2})(x + y) = {x^3} + {x^2}y - {x^2}y - x{y^2} + {y^2}x + {y^3} = {x^3} + {y^3}

Bài 9 (tr.8 SGK)

Hướng dẫn:

Rút gọn biểu thức sau đó thay giá trị của x, y vào biểu thức đã rút gọn để tính giá trị biểu thức nhanh hơĩi.

Rút gọn biểu thức:

(x – y)({x^2}  + xy + {y^2} ) ={x^3}  + {x^2} y + x{y^2}  – {x^2} y – x{y^2}  – {y^3}  = {x^3}  – {y^3}

Ta có kết quả sau:

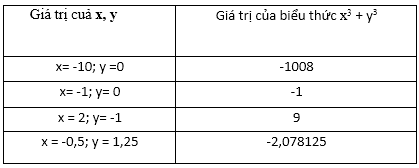
Bài 10 (tr.8 SGK)

a)

({x^2} - 2x + 3)(\frac{1}{2}x - 5) = \frac{1}{2}{x^3} - 5{x^2} + 10x + \frac{3}{2}x - 15

= \frac{1}{2}{x^3} - 6{x^2} + \frac{{23}}{2}x - 15.

b)

({x^2} - 2xy + {y^2})(x - y) = {x^3} - {x^2}y - 2{x^2}y + 2x{y^2} + x{y^2} - {y^3}

= {x^3} - 3{x^2}y + 3x{y^2} - {y^3}

Bài 11 (tr. 8 SGK)

Hướng dẫn:

Ta biến đổi biểu thức đã cho thành một biểu thức không còn chứa biến.

Giải:

Thực hiện phép nhân đa thức và rút gọn ta được:

(x – 5)(2x + 3) – 2x(x – 3) + X + 7 = 2{x^2}  + 3x – 10x – 15 – 2{x^2}  + 6x + x + 7 = -8

Ta thấy giá trị của biểu thức trên luôn luôn bằng -8 với mọi giá trị của biến x.

Vậy, giá trị của biểu thức đã cho không phụ thuộc vào giá trị của biến x.

Bài 12 (tr. 8 SGK)

Hướng dẫn:

Rút gọn biểu thức sau đó thay giá trị của X vào biểu thức đã rút gọn.

Giải:

Rút gọn biểu thức:

({x^2}  – 5)(x + 3) + (x + 4)(x – {x^2} )

= {x^3}  + 3{x^2}  – 5x – 15 + {x^2}  – {x^3}  + 4x – 4{x^2}  = -x – 15.

Bài 13 (tr. 9 SGK)

Hướng dẫn:

Thực hỉện phép nhân đa thức, biến đổi và rút gọn đẳng thức về dạng:

ax = b từ đó x = –\frac{b}{a } (nếu a  ≠ 0).

Giải:

(12x – 5)(4x – 1) + (3x – 7)(1 – 16x) = 81

<=>48{x^2}  – 12x – 20x + 5 + 3x – 48{x^2}  – 7 + 112x = 81

<=> 83x – 2 = 81

<=> 83x = 83

<=> x = 1.

Bài 14 (tr. 9 SGK)

Hướng dẫn:

Gọi ba số tự nhiên chẵn liên tiếp phải tìm là x , x + 2 , x + 4 (x € N).

Ta có: (x + 2)(x + 4) – x(x + 2) = 192.

Tìm được x = 46.

Giải:

Gọi ba số tự nhiên chẵn liên tiếp phải tìm là x , x + 2 , x + 4 (x € N).

Tích hai số đầu là: x(x + 2)

Tích hai số sau là: (x + 2)(x + 4)

Theo    đề bài ta có:  (x + 2)(x + 4) – x(x + 2) = 192

<=>{x^2}  + 4x + 2x + 8 – {x^2}  – 2x= 192

<=> 4x + 8  = 192

<=> 4x = 184

<=> x =  46

Vậy,  ba số tự nhiên chẵn liên tiếp cần tìm là: 46, 48,  50.

Bài 15 (tr.9 SGK)

a)

(\frac{1}{2}x + y)(\frac{1}{2}x + y) = \frac{1}{4}{x^2} + \frac{1}{2}xy + {y^2} = \frac{1}{4}{x^2} + xy + {y^2}

b)

(x - \frac{1}{2}y)(x - \frac{1}{2}y) = {x^2} - \frac{1}{2}xy + \frac{1}{4}{y^2} = {x^2} - xy + \frac{1}{4}{y^2}

Đang tải...

Bài mới

loading...

Trackbacks

  1. Bài tập phần: Nhân đơn thức với đa thức - Toán lớp 8- Hoc360.net | Học Online
  2. bài tập phần những hằng đẳng thức đáng nhớ sách giáo khoa Toán lớp 8 | Học Online

Bình luận

© Hoc360.net. All rights reserved.

Chính sách bảo mật. Quy định sử dụng . Liên hệ .

Email: hoc360net@gmail.com

Mobile: 09026788686

Địa chỉ: Số nhà 20 ngõ 140 Tôn Thất Tùng, Phường Khương Thượng, Quận Đống Đa, Thành phố Hà Nội