ĐỀ THI TUYỂN SINH LỚP 10 CHUYÊN TOÁN Quốc HỌC HUẾ
Năm học 2005-2006
Thời gian: 150 phút
Bài 1:
a) Cho a, b là các số thực không âm tùy ý.
Chứng tỏ rằng: ≤
+
≤
. Khi nào có dấu đẳng thức?
b) Xét u, v , z, t là các số thực không âm thay đổí có tổng bằng 1. Hãy tìm giá trị lớn nhất và giá trị nhỏ nhất của:
S = +
+
+
Bài 2:
Cho tam ADEH có độ dài hai cạnh góc vuông là DE = 5cm và EH = 12cm.
a) Tính độ dài bán kính đường tròn nội tiếp tam giác vuông DEH.
b) Trong tam giác vuông DEH có hai đường tròn có cùng bán kính r, tiếp xúc ngoài nhau và tiếp xúc với các cạnh tam giác vuông DEH như hình dưới. Tính độ dài của r.
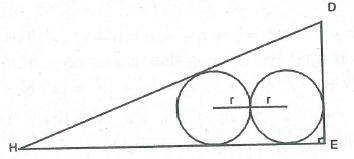
Bài 3:
a) Tìm tất cả các nghiệm nguyên của phương trình:
2x + 9y = 2005 (*).
b) Chứng minh rằng: x.y ≤ 55833 trong đó (x, y) là nghiệm nguyên bất kì của (*).
Bài 4:
Với mỗi giá trị của tham số m, xét hàm số: y = – 2mx – 1 –
.
a) Chứng tỏ với giá trị m tùy ý, đồ thị hàm số trên luôn cắt trục tung tại một điểm A, cắt trục hoành tại hai điểm phân biệt B, C và các giao điểm này đều khác gốc tọa độ O.
b) Đường tròn đi qua các giao điểm A, B, C cắt trục tung thêm một điểm K khác A. Chứng minh rằng khi m thay đổi, K là một điểm cố định.
Bài 5:
Có 8 cái hộp, mỗi hộp chứa 6 trái banh. Chứng tỏ rằng có thể ghi số trên tất cả các trái banh sao cho thỏa đồng thời ba điều kiện sau:
1) Mỗi banh được ghi đúng một số nguyên, chọn trong các số nguyên từ 1 đến 23.
b) Trong mỗi hộp, không có hai banh nào được ghi cùng một số.
Với hai hộp bất kì, có nhiều nhất một số xuất hiện đồng thời ở cả hai hộp.




Comments mới nhất