Các định nghĩa vectơ – Sách bài tập toán 10 – Bài tập Hình học

Các định nghĩa vectơ

A. CÁC KIẾN THỨC CẦN NHỚ

1. Để xác định một vectơ cần biết một trong hai điều kiện sau :

• Điểm đầu và điểm cuối của vectơ;
• Độ dài và hướng của vectơ.

2. Hai vectơ và được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

Nếu hai vectơ và cùng phương thì chúng có thể cùng hướng hoặc ngược hướng.

3. Độ dài của một vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó. Độ dài của được kí hiệu là || , I| = AB.

4.  =  khi và chỉ khi || = ||  và , ) cùng hướng.

5. Với mỗi điểm A ta gọi là vectơ – không. Vectơ – không được kí hiệu là 0, do đó ll = 0 và ta quy ước rằng vectơ 0 cùng phương, cùng hướng với mọi vectơ.

B. DẠNG TOÁN CƠ BẢN

VẤN ĐỀ 1

Xác định một vectơ, sự cùng phương hướng của hai vectơ

1. Phương pháp

Để xác đinh vectơ ≠ 0 ta cần biết || và hướng của hoặc biết điểm đầu và điểm cuối của . Chẳng hạn, với hai điểm phân biệt Avà B ta có hai vectơ khác vectơ là và 

Vectơ là vectơ – không khi và chỉ khi || = 0 hoặc = vói Alà điểm bất kì.

2. Các ví dụ

Ví dụ 1. Cho 5 điểm phân biệt A, B, C, D và E. Có bao nhiêu vectơ khác vectơ – không có điểm đầu và điểm cuối là các điểm đã cho ?

GIẢI

Với hai điểm phân biệt, chẳng hạn Avà B, có hai vectơ và . Với 5 điểm phân biệt đã cho, ta có 10 tập hợp khác nhau, cụ thể là :

{A,B},[A,C},{A,D},{A,E},{B,C},{B,D},{B,E},{C,D},{C,E},{D,E}.

Do đó ta có 20 vectơ (khác ) có điểm đầu và điểm cuối là 5 điểm đã cho.

Cách khác : Một vectơ được xác định khi biết điểm đầu và điểm cuối của nó. Với 5 điểm phân biệt, ta có 5 cách chọn điểm đầu. Với mỗi cách chọn điểm đầu ta có 4 cách chọn điểm cuối. Vậy số vectơ khác là : 5 × 4 = 20 (vectơ).

Ví dụ 2. Cho điểm A và vectơ khác . Tìm tập hợp các điểm M sao cho :

a) cùng phương với ;

b) cùng hướng với .

GIẢI

 

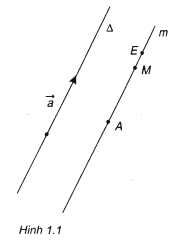
Gọi Δ là giá của a(h.1.1).

Nếu cùng phương với thì đường thẳng AM song song với Do đó M thuộc đường thẳng m đi qua A và song song vói Δ.

Ngược lại, mọi điểm M thuộc đường thẳng m thì cùng phương với .

Chú ý rằng nếu A thuộc đường thẳng A thì m trùng vói À.

b) Lập luận tương tự như trên, ta thấy các điểm M thuộc một nửa đường thẳng gốc A của đường thẳng Cụ thể, đó là nửa đường thẳng có chứa điểm

E sao cho và cùng hướng.

VẤN ĐỀ 2

Chứng minh hai vectơ bằng nhau

1. Phương pháp

Để chứng minh hai vectơ bằng nhau ta có thể dùng một trong ba cách sau:

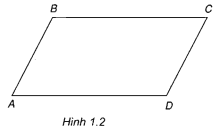
• Tứ giác ABCD là hình bình hành ⇒  =  và  =  (h.1.2).
• Nếu  = ,  =  thì  = 

2. Các ví dụ

Ví dụ 1. Cho tam giác ABC có D, E, F lần lượt là trung điểm BC, CA, AB. Chứng minh  = 

GIẢI

 

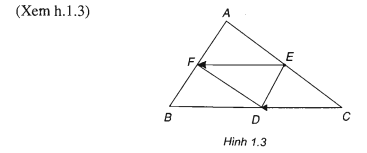
Vì EF là đường trung bình của tam giác ABC nên EF = BC = CD và EF // CD.

Do đó tứ giác EFDC là hình bình hành, nên  = 

Ví dụ 2.  Cho hình bình hành ABCD. Hai điểm M và N lần lượt là trung điểm của BC và AD. Điểm I là giao điểm của AM và BN, K là giao điểm của DM và CN. Chứng minh = , = .

GIẢI

 

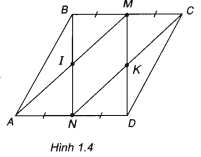
Tứ giác AMCN là hình bình hành vì MC= AN và MC // AN. Suy ra

= (h.1.4).

Vì MCDN là hình bình hành nên K là trung điểm của MD. Suy ra

= .Tứ giác IMKN là hình

bình hành, suy ra NI = KM.Do đó  = .

Ví dụ 3. Chứng minh rằng nếu hai vectơ bằng nhau có chung điểm đầu (hoặc điểm cuối) thì chúng có chung điểm cuối (hoặc điểm đầu).

GIẢI

Giả sử = . Khi đó AB = AC,ba điểm A, B, c thẳng hàng và B, C thuộc một nửa đường thẳng gốc A.Do độ B ≡ C.

Nếu hai vectơ bằng nhau có chung điểm cuối thì chúng có chung điểm đầu được chứng minh tương tự.

Ví dụ 4. Cho điểm A và vectơ . Dựng điểm M sao cho :

a) = ;

b) cùng phương với và có độ dài bằng ||.

GIẢI

 

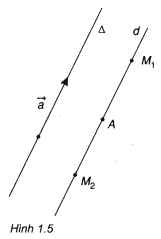
Gọi Δ là giá của vectơ . Vẽ đường thẳng d đi qua A và d // Δ (nếu điểm A thuộc Δ thì d trùng với Δ). Khi đó có hai điểm và  thuộc đường thẳng d sao cho (h.1.5). Ta có :

và cùng phương với và có độ dài bằng độ dài của .

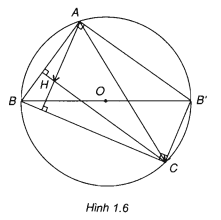
Ví dụ 5. Cho tam giác ABC có H là trực tâm và O là tâm đường tròn ngoại tiếp. Gọi B’ là điểm đối xứng của B qua O. Chứng minh = .

GIẢI

Vì BB’ là đường kính của đường tròn ngoại tiếp tam giác ABC nên = = 90°. Do đó CH // B’A và AH // B’C. Suy ra tứ giác AB’CH là hình bình hành. Vậy = .(h.1.6).

C. CÂU HỎI VÀ BÀI TẬP

1.1. Hãy tính số các vectơ (khác ) mà các điểm đầu và điểm cuối được lấy từ các điểm phân biệt đã cho trong các trường hợp sau :

a) Hai điểm;

b) Ba điểm;

c) Bốn điểm.

⇒ Xem đáp án tại đây.

1.2. Cho hình vuông ABCD tâm O. Liệt kê tất cả các vectơ bằng nhau (khác ) nhận đỉnh và tâm của hình vuông làm điểm đầu và điểm cuối.

⇒ Xem đáp án tại đây.

1.3. Cho tứ giác ABCD. Gọi M, N, P và Q lần lượt là trung điểm của các cạnh AB, BC, CD và DA. Chứng minh = và = .

⇒ Xem đáp án tại đây.

1.4. Cho tam giác ABC. Các điểm M và N lần lượt là trang điểm các cạnh AB và AC so sánh độ dài của hai vectơ và . Vì sao có thể nói hai vectơ này cùng phương ?

⇒ Xem đáp án tại đây.

1.5. Cho tứ giác ABCD, chứng minh rằng nếu = thì = .

⇒ Xem đáp án tại đây.

1.6. Xác định vị trí tương đối của ba điểm phân biệt A, B và C trong cậc trường hợp sau:

a) và cùng hướng, || > ||

b) và ngược hướng ;

c) và cùng phương.

⇒ Xem đáp án tại đây.

1.7. Cho hình bình hành ABCD. Dựng = , = , = , = . Chứng minh = .

⇒ Xem đáp án tại đây.