Các dạng toán cơ bản về khối đa diện – Sách bài tập Hình học 12
♦Vấn đề 1:
Chứng minh một số tính chất liên quan đến các đỉnh, các cạnh,, các mặt của một khối đa diện
1. Phương pháp giải
Sử dụng tính chất a) và b) trong định nghĩa hình đa diện.
2. Ví dụ
Chứng minh rằng một đa diện mà mỗi đỉnh của nó đều là đỉnh chung của đúng ba mặt thì tổng số các đỉnh của nó phải là một số chẵn. Cho ví dụ.
Giải
Gọi d là số các đỉnh của một khối đa diện (H). Vì mỗi đỉnh của nó đều là đỉnh chung của đúng ba mặt, nên mỗi đỉnh của nó có đúng ba cạnh đi qua. Như vậy qua d đỉnh có 3d cạnh. Nhưng do mỗi cạnh nối đúng hai đỉnh nên số các
cạnh của (H) bằng .
Suy ra d phải là số chẵn.
Ví dụ : Hình tứ diện, hình hộp.
♦Vấn đề 2:
Chứng minh hai đa diện bằng nhau
1. Phương pháp giải
Chỉ ra một phép dời hình cụ thể đã được xác định biến đa diện này thành đa diện kia.
2. Ví dụ
Cho lăng trụ ABCDEF.A’B’C’D’E’F’ có đáy là những lục giác đều. Gọi I là trung điểm của đoạn thẳng nối hai tâm của đáy. Gọi (a) là mặt phẳng đi qua / và cắt tất cả cạnh bên của lăng trụ. Chứng minh rằng (a) chia lăng trụ thành hai đa diện bằng nhau.
Giải
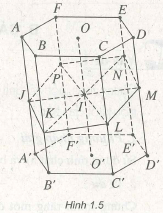
Giả sử mp (α) cắt AA’ , BB’ , CC’ , DD’, EE’ , FF’ lần lượt tại J, K, L, M, N, p (h.1.5). Dễ thấy
I cũng là trung điểm của JM, KN và Phép đối xứng tâm I biến các điểm A, B, c, D, E, F, J, K,
L, M, N, P lần lượt thành các điểm D’, E’ , F’ , , A’, B’ , C’, M, N, P, J, K, L. Do đó hai đa diện
ABCDEF JKLMNP và D’E’F’A’B’C’.MNPJKL bằng nhau vì có phép dời hình là phép đối xứng
tâm I biến đa diện này thành đa diện kia.
Xem thêm: Câu hỏi và bài tập khối đa diện tại đây.
♦Vấn đề 3:
Phân chia hoặc lắp ghép các khối đa diện
1. Phương pháp giải
Chọn mặt phẳng thích hợp để phân chia khối đa diện. Trong nhiều trường hợp, để chứng minh rằng có thể lắp ghép các khối đa diện (H1), (H2) … , (Hn) thành khối đa diện (H) ta chứng minh rằng có thể chia được khối đa diện (H) thành các khối đa diện (H1), (H2) … , (Hn).
2. Ví dụ
Cho hình chóp tứ giác F.ABCD có đáy là hình vuông. Cạnh bên FC vuông góc với đáy và có độ dài bằng AB. Chứng minh rằng có thể dùng ba hình chóp bằng hình chóp trên để ghép lại thành một hình lập phương.
Giải
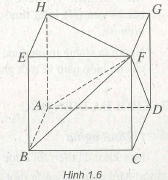
Từ hình chóp trên ta dựng hình lập phương HEFG.ABCD (h. 1.6). Ta thấy hai hình chóp
F.ABCD và F.ABEH đối xứng với nhau qua mặt phẳng (ABF), hai hình chóp F.ABCD và
F.AHGD đối xứng với nhau qua mặt phẳng (ADF). Do đó ba hình chóp F.ABCD, F.ABEH và
F.AHGD bằng nhau.
Như vậy có thể chia được hình lập phương HEFG.ABCD thành ba hình chóp bằng hình chóp
F.ABCD. Từ đó suy ra có thể ghép ba hình chóp bằng hình chóp F.ABCD để thành một hình
lập phương.
Nhận xét :
Để ý rằng phép đối xứng qua mặt phẳng (FAC) biến tứ diện FACB thành tứ diện FACD, do
đó có thể chia hình chóp F.ABCD thành hai tứ diện bằng nhau : FACB và FACD. Làm tương tự
đối với hai hình chóp F.ABEH và F.AHGD suy ra có thể chia một hình lập phương thành sáu
hình tứ diện bằng nhau.. (Bài tập 4, trang 12, SGK)




Trackbacks