Khái niệm về thể tích của khối đa diện – Các dạng toán cơ bản – Sách bài tập Hình học 12
VẤN ĐỀ 1:
Tính thể tích của một khối đa diện
1 . Phương pháp giải
a) Chia khối đa diện đã cho thành các khối lăng trụ hoặc các khối chóp đơn giản hơn.
b) Ghép thêm vào khối đa diện đã cho các khối đa diện quen biết để được một khối đa diện đơn giản hơn.
c) Tìm tỉ số thể tích giữa khối đa diện đã cho với một khối đa diện đã biết thể tích.
2. Ví dụ
Ví dụ 1. Cho hai đoạn thẳng AB và CD chéo nhau. AB = a, CD = b, khoảng cách giữa chúng bằng h, góc giữa chúng bằng a. Tính thể tích của tứ diện ABCD.
Giải
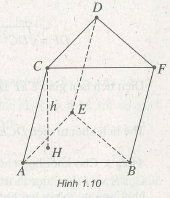
Dựng các hình bình hành ACDE và CABF.
Ta được hình lăng trụ ABE.CFD. (h.1.10)
Ta có : h = d(AB, CD) = d((ABE), (CDF)) = chiều cao lăng trụ.
Hai hình chóp B.ACD và F.ACD có cùng đáy và chiều cao nên :
![]()
Hình chóp F.ACD và lăng trụ có cùng đáy ACD và chiều cao nên:
![]()
Vậy:
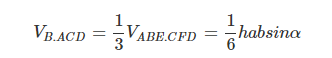
Ví dụ 2. Cho khối hộp chữ nhật ABCD.A’B’C’D’ có A5 = a, 5C = b, AA’ = c. Gọi E và F lần lượt là trung điểm của B’C’ và C’D’. Mặt phẳng (AEF) chia khối hộp đó thành hai khối đa diện (H) và trong đó (H) là khối đa diện chứa đỉnh A’. Tìm thể tích của (H) và (Hr).
Giải
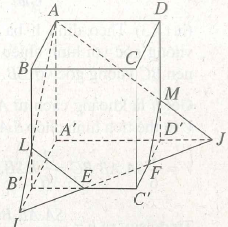
Giả sử đường thẳng EF cắt đường thẳng A’B’ tại I và cắt đường thẳng A’D’ tại J. AI cắt BB’ tại L, AJ cắt DD’ tại M.
Gọi (K) là tứ diện AA’IJ.
Khi đó :
![]()
Vì EB’ – EC’ và B’I // C’F
nên B’I = C’F = A’B’/2. Tương tự, D’J = A’D’/2.
Từ đó theo định lí Ta-lét ta có:
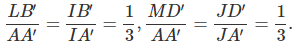
Do đó:
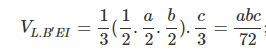
Tương tự:
![]()
Vì
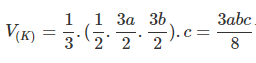
![]()
Xem thêm: Câu hỏi và bài tập phần thể tích của khối đa diện tại đây.
VẤN ĐỀ 2:
Dùng cách tính thể tích để giải một số bài toán hình học
1. Phương pháp giải
a) Tính các đại lượng hình học của khối đa diện theo thể tích của khối đa diện ấy.
b) Dùng hai cách để tính thể tích của cùng một khối đa diện rồi so sánh chúng với nhau để rút ra đại lượng hình học cần tìm.
2. Ví dụ
Ví dụ 1 . Cho hình chóp tam giác S.ABC có đáy là tam giác vuông ở B. Cạnh SA vuông góc với đáy. Biết rằng AB -a, SA = b.
Hãy tính khoảng cách từ A đến mặt phẳng (SBC).
Giải
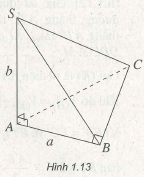
Theo định lí ba đường vuông góc, BC vuông góc với hình chiếu AB của đường xiên SB nên BC vuông góc với SB.
Gọi h là khoảng cách từ A đến mặt phẳng (SBC), V là thể tích hình chóp ABC thì:
![]()
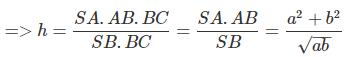
Ví dụ 2. Cho tứ diện ABCD và M là một điểm trong của tứ diện đó. Gọi hA, hB, hc, hD lần lượt là khoảng cách từ A, B, c, D đến các mặt đối diện và mA, mB, mc, mD lần lượt là khoảng cách từ M đến các mặt (BCD), (CDA), (DAB),(ABC). Chứng minh rằng:
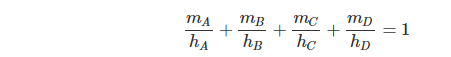
Giải
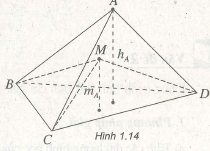
Gọi thể tích các khối tứ diện ABCD, MBCD, MCDA, MDAB, MABC theo thứ tự là VA, VB, VC, VD, ta có:
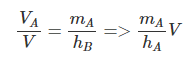
Tương tự:
![]()
Do đó:
![]()
Từ đó suy ra:
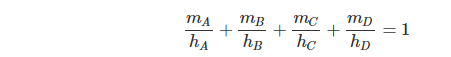
VẤN ĐỀ 3:
Tìm tỉ số thể tích của hai khối đa diện
1. Phương pháp giải
a) Tính thể tích của từng khối đa diện.
b) Sử dụng chú ý ii) với công thức :
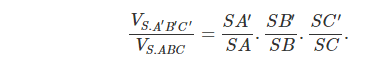
2. Ví dụ
Cho hình chóp tứ giác đều S.ABCD. Mặt phẳng (P) qua A và vuông góc với SC
cắt SB, SC, SD lần lượt tại B’, C’, D’ . Biết rằng AB = a, SB’/SB = 2/3.
a) Tính tỉ số thể tích của hai khối chóp AB ‘C ‘D ‘ và S.ABCD.
b) Tính thể tích của khối chóp S.AB’C’D’.
Giải
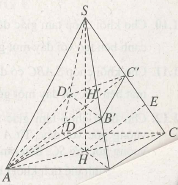
Gọi SH là đường cao của hình chóp tứ giác đều S.ABCD, SH cắt (P) tại H’. Khi đó H là giao của AC và BD. Vì BD⊥ (SAC) nên BD ⊥ SC. Do đó BD // (P). Từ đó suy ra (P) cắt (SDB) theo giao tuyến B’D’ song song với BD. Do đó : SD’/SD = SH’/SH = SB’/SB = 2/3, H’B’ = H’D’ và D’B’ ⊥ AC’ .
Giả sử đường thẳng qua H song song với AC’ cắt sc tại E. Khi đó EC’ = EC , SC’/SE =2/3.
Từ đó suy ra:
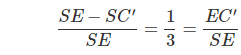
Do đó: SC’ = 2EC’ =C’C.
Ta có:
![]()
Từ đó suy ra:
![]()
Vậy:
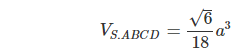
b) Theo chứng minh trên ta có AC’ vừa là đường cao, vừa là trung tuyến của tam giác SAC nên AS = AC . Do đó tam giác SAC đều. Từ đó suy ra:

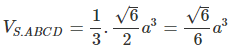
Từ đó suy ra:
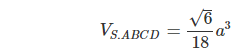




Trackbacks